
题目列表(包括答案和解析)
2.选择题:
①如果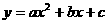 的图象经过(1,4),(0,2)和(-2,-8)三点,则
的图象经过(1,4),(0,2)和(-2,-8)三点,则 的值是:
的值是:
A. 4 B. 0 C. 6 D. -6
②
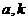 同号,
同号, 异号,在同一直角坐标系中二次函数
异号,在同一直角坐标系中二次函数 与一次函数
与一次函数 的图象大致是:
的图象大致是:
y y y y
0 x 0 x 0 x 0 x
A. B. C. D.
③二次函数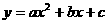 的图象如图所示,则
的图象如图所示,则 的值是:
的值是:
A. B.
B.
C. D.
D.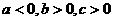
④抛物线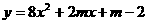 的顶点在
的顶点在 轴上,则顶点坐标是:
轴上,则顶点坐标是:
A.(4,0) B.(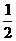 ,0)
C.(-
,0)
C.(-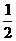 ,0)
D.(0,
,0)
D.(0,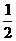 )
)
⑤要使关于 的方程
的方程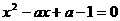 的两根的平方根最小,则
的两根的平方根最小,则 等于:
等于:
A. 0 B. –1 C. 1 D. 2
1.填空题:
⑴将 的图象向上平移3个单位,得到函数______的图象,其顶点坐标是______,对称轴方程是______.
的图象向上平移3个单位,得到函数______的图象,其顶点坐标是______,对称轴方程是______.
⑵将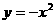 的图象向右平移3个单位,再向上平移4个单位,得到函数______的图象,顶点坐标是______,对称轴是______.
的图象向右平移3个单位,再向上平移4个单位,得到函数______的图象,顶点坐标是______,对称轴是______.
⑶函数 的图象的顶点关于
的图象的顶点关于 轴的对称点的坐标是______.
轴的对称点的坐标是______.
⑷ 中,
中, ,则它的开口向______.顶点在第______象限
,则它的开口向______.顶点在第______象限
⑸将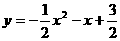 配方成
配方成 的形式是____________.顶点坐标是______,对称轴是______.
的形式是____________.顶点坐标是______,对称轴是______.
⑹抛物线 与
与 轴的交点坐标是______,与
轴的交点坐标是______,与 轴交点坐标是______.
轴交点坐标是______.
⑺二次函数 有最小值-4,且图象的对称轴在
有最小值-4,且图象的对称轴在 轴的右侧,则
轴的右侧,则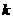 的值是______.
的值是______.
⑻ 交于A,B,顶点是C,则S△ABC=______.
交于A,B,顶点是C,则S△ABC=______.
⑼ 与
与 轴交于A,B,与
轴交于A,B,与 轴交于C,则S△ABC=______.
轴交于C,则S△ABC=______.
⑽已知二次函数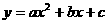 的图象经过(1,3)和(0,4)及(2,6)三点,则二次函数解析式是____________.
的图象经过(1,3)和(0,4)及(2,6)三点,则二次函数解析式是____________.
⑾抛物线 与
与 轴交于A,B两点,B在A的右侧,点P是抛物线在
轴交于A,B两点,B在A的右侧,点P是抛物线在 轴上方部分的一点,且S△ABP=6,则A点坐标是______,B点坐标是______,P点坐标是______.
轴上方部分的一点,且S△ABP=6,则A点坐标是______,B点坐标是______,P点坐标是______.
⑿已知二次函数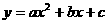 的图象经过(1,1),还经过一次函数
的图象经过(1,1),还经过一次函数 的图象与
的图象与 轴,
轴, 轴的交点,则函数解析式为______,顶点坐标是______.
轴的交点,则函数解析式为______,顶点坐标是______.
⒀已知二次函数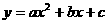 的图象经过(-1,-
的图象经过(-1,- ),B(0,-4),C(4,0)三点,则二次函数的解析式是______,顶点D的坐标是______,对称轴方程是______,
),B(0,-4),C(4,0)三点,则二次函数的解析式是______,顶点D的坐标是______,对称轴方程是______,
S四边形OBDC=______
6.求解二次函数的图象,应先求出顶点坐标,对称轴方程,然后按照对称性列表、描点、连线.
如:解出 的图象.
的图象.
解:顶点坐标是(-3,2),对称轴是 .
.
列表,得:
 |
… |
-6 |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
 |
… |
- |
0 |
 |
2 |
 |
0 |
 |
描点、连线,得:
 y
y

x

5.抛物线的顶点是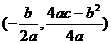 ,也可写成
,也可写成 .
.
 ①若
①若 >0,
>0, >0,则
>0,则 ,即顶点的纵坐标为负,则顶点在
,即顶点的纵坐标为负,则顶点在 轴下方,而抛物线向上伸展,所以抛物线一定与
轴下方,而抛物线向上伸展,所以抛物线一定与 轴相交.
轴相交.
0 x
 ②若
②若 >0,
>0,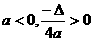 ,顶点在
,顶点在 轴上方,抛物线向下伸展,则抛物线与
轴上方,抛物线向下伸展,则抛物线与 轴也一定有两个交点. y
轴也一定有两个交点. y
0 x
③若 =0,无论
=0,无论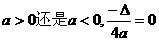 .即顶点在
.即顶点在 轴上,抛物线与
轴上,抛物线与 轴只有一个交点.
轴只有一个交点.
 ④若
④若 <0,
<0, ,顶点在
,顶点在 轴上方,而抛物线向上伸展,故与
轴上方,而抛物线向上伸展,故与 轴不相交. y
轴不相交. y
0 x y
 ⑤若
⑤若 <0,
<0,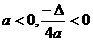 ,抛物线向下伸展,所以抛物线与
,抛物线向下伸展,所以抛物线与 轴不相交.
轴不相交.
0
所以,(1) >0
>0 抛物线
抛物线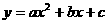 一定与
一定与 轴有两个交点.
轴有两个交点.
(2) =0,抛物线与
=0,抛物线与 轴有一个交点.
轴有一个交点.
(3) <0,抛物线与
<0,抛物线与 轴没有交点.
轴没有交点.
判断抛物线与 轴有无交点,就是判定
轴有无交点,就是判定 的值是正还是负.
的值是正还是负.
再例如求 与
与 轴的交点坐标,因交点在
轴的交点坐标,因交点在 轴上,也在抛物线上,所以纵坐标
轴上,也在抛物线上,所以纵坐标 ,即
,即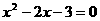 ,
, ;所以与
;所以与 轴交点坐标是(3,0)和(-1,0).这说明求抛物线
轴交点坐标是(3,0)和(-1,0).这说明求抛物线 轴的交点坐标,就要求
轴的交点坐标,就要求 的根
的根 ,交点坐标是(
,交点坐标是(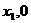 )和(
)和( ),而求
),而求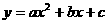 与
与 轴的交点坐标,就是
轴的交点坐标,就是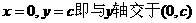 .
.
4.抛物线的顶点坐标、对称轴方程的求法有2种:一种是将 配方成
配方成 的形式,如:
的形式,如:

= ……(加上并减去一次项系数的一半的平方)
……(加上并减去一次项系数的一半的平方)
=
=
所以顶点是(-3,2),对称轴是 .
.
另一种是直接套用公式.顶点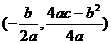 ,对称轴是
,对称轴是 .因同学们配方不太熟练,准确性不高;因此最好用公式求,尤其是当系数是整数时.
.因同学们配方不太熟练,准确性不高;因此最好用公式求,尤其是当系数是整数时.
3. 和
和 ,通过解析式我们得知,对于同一个自变量
,通过解析式我们得知,对于同一个自变量 的值,
的值, 的值总比
的值总比 的值大或小|
的值大或小| |个单位.(如
|个单位.(如 .对于每一个
.对于每一个 的值,
的值, 的值总比
的值总比 的值小于3个单位.而
的值小于3个单位.而 ,对于同一个
,对于同一个 的值
的值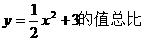
 的值大3个单位)这一特点反映在函数图象上就是将
的值大3个单位)这一特点反映在函数图象上就是将 的图象上的各点向上平移|
的图象上的各点向上平移| |个单位.(
|个单位.(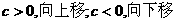 )此时
)此时 的对称轴仍是
的对称轴仍是 轴,而顶点坐标是(0,
轴,而顶点坐标是(0, ),它的开口方向与
),它的开口方向与 的图象的开口一样,
的图象的开口一样, ;而
;而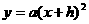 的图象与
的图象与 的图象各点具有对于同一个
的图象各点具有对于同一个 值,
值, 值不同,譬如
值不同,譬如 列表:
列表:
 |
… |
-6 |
-5 |
-4 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
 |
… |
|
|
|
 |
2 |
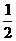 |
0 |
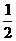 |
2 |
 |
 |
… |
 |
2 |
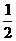 |
0 |
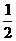 |
2 |
 |
|
|
|
对于同一个 ,在
,在 中,
中, 对应的
对应的 是-3和3,在
是-3和3,在 中,
中,  对应的
对应的 值是-6和0.而-6比-3小3个单位,0比3小3个单位,这说明:对于同一个
值是-6和0.而-6比-3小3个单位,0比3小3个单位,这说明:对于同一个 所对应的
所对应的 值,总比
值,总比 所对应的
所对应的 值小3个单位.
值小3个单位.
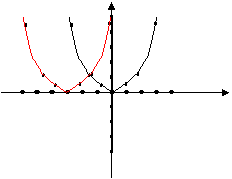 y
y
x
这些特性反映在图象上就是将 图象上各点向左平移3个单位得到函数
图象上各点向左平移3个单位得到函数 的图象上的点,函数
的图象上的点,函数 的图象整个向左平移3个单位得到
的图象整个向左平移3个单位得到 的图象.同理,将
的图象.同理,将 的图象向右平移2个单位得到
的图象向右平移2个单位得到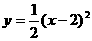 的图象,总之将
的图象,总之将 的图象向左或向右平移|h|个单位(h>0时向左移动;h<0时,向右移)就得到
的图象向左或向右平移|h|个单位(h>0时向左移动;h<0时,向右移)就得到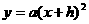 的图象,由于图象左右移动,对称轴发生变化,不是
的图象,由于图象左右移动,对称轴发生变化,不是 轴了,而是直线
轴了,而是直线 ,顶点是(
,顶点是( 0).
0).
由于 的图象是将
的图象是将 的图象向上平移2个单位,而
的图象向上平移2个单位,而 是由
是由 的图象向左平移3个单位,所以
的图象向左平移3个单位,所以 是由
是由 的图象向左平移3个单位,再向上平移2个单位得到的,其顶点是(-3,2),对称轴是
的图象向左平移3个单位,再向上平移2个单位得到的,其顶点是(-3,2),对称轴是 .
.
2.二次函数 的图象是顶点在原点的抛物线.其性质是
的图象是顶点在原点的抛物线.其性质是 时,抛物线的开口向上;
时,抛物线的开口向上; 时,抛物线的开口向下;对称轴是
时,抛物线的开口向下;对称轴是 轴;顶点坐标是(0,0);
轴;顶点坐标是(0,0); 时,
时, =0;
=0; =0.
=0.
1.函数 叫做二次函数.
叫做二次函数.
4.会画二次函数的图象,能解较复杂的二次函数题目.
3.会求二次函数的顶点坐标,对称轴方程及最大值或最小值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com