1、如图所示，图中共有　 条线段，共有　　 个长方形。毛

24. (本题有3小题，第(1)小题5分，第(2)小题①4分，第(2)小题②5分，满14分)

　 　已知抛物线y=x²+(2n-1)x+n²-1 (n为常数).

(1)当该抛物线经过坐标原点，并且顶点在第四象限时，求出它所对应的函数关系式；

(2)设A是(1)所确定的抛物线上位于x轴下方、且在对称轴左侧的一个动点，过A作x轴的平行线，交抛物线于另一点D，再作AB⊥x轴于B，DC⊥x轴于C.

　　 ①当BC=1时，求矩形ABCD的周长；

　　 ②试问矩形ABCD的周长是否存在最大值？如果存在，请求出这个最大值，并指出此时A点的坐标；如果不存在，请说明理由.

23．如果一个正整数能表示为两个连续偶数的平分差，那么

　称这个正整数为“神秘数”．如：，

　　　　　　　　　　　　　　 　，

　　　　　　　　　　　　　　 　，

　因此4，12，20都是“神秘数”

　(1)28和2 012这两个数是“神秘数”吗？为什么？

　(2)设两个连续偶数为2k+2和2k(其中k取非负整数)，由这两个连续偶数构造的神秘数是4的倍数吗？为什么？

　(3)两个连续奇数的平方数(取正数)是神秘数吗？为什么？

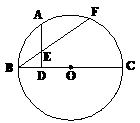
22．如图，已知⊙O中，BC是直径，D点为OB上任意一点(异于O、B)

⌒　 ⌒

过D点作AD⊥BC，交⊙O于点A。 AB = AF，连结BF交AD于E点。

(1)探究AE与BE的大小关系，并证明你的结论；

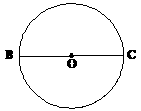
(2)当D为OC上任意一点(异于O、C)，其它条件不变时，(1)中的结论是否仍然成立，画出图形并证明你的结论。

20.如图，反比例函数图象在第一象限的分支上有一点C(1，3)，过点C的直线y = kx + b(k < 0)与x轴交于点A.

(1)求反比例函数的解析式；

(2)当直线与反比例函数的图象在第一象限内的另一交点的横坐标为3时，求△COA的面积.

○21．如图，四边形ABCD是菱形，CE⊥AB，交AB的延长线于E，CF⊥AD，交AD的延长线于F。请你猜猜CE与CF的大小有什么关系？并证明你的猜想.

☆21. 如图，在△ABC中，∠C=90°，AC=6，BC=8，M是BC的中点，P为AB上的一个动点，(可以与A、B重合)，并作∠MPD=90°，PD交BC(或BC的延长线)于点D.

(1)记BP的长为x，△BPM的面积为y，求y关于x的函数关系式，并写出自变量x的取值范围；

(2)是否存在这样的点P，使得△MPD与△ABC相似？若存在，请求出x的值；若不存在，请说明理由.

19. 现有一张长和宽之比为2：1的长方形纸片，将它折两次(第一次折后也可打开铺平再折第二次)，使得折痕将纸片分为面积相等且不重叠的四个部分(称为一次操作)，如图甲(虚线表示折痕)．除图甲外，请你再给出三种不同的操作，分别将折痕画在图①至图③中(规定：一个操作得到的四个图形，和另一个操作得到的四个图形，如果能够“配对”得到四组全等的图形，那么就认为是 相同的操作，如图乙和图甲示相同的操作)．

(甲)　　　　　　　　　　　　　　 (乙)

　　　 ①　　　　　　　　　　　　 ②　　　　　　　　　　 ③

18. (本题8分)如图，点D、C在BF上，

AB∥EF，∠A=∠E，BC=DF，

　　 求证AB=EF．

(注：带“○”号二中学生做，带“☆”实验及七班学生做)

17.(本小题8分)(1)(1+)÷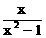； (2)|－2|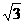－(－1)⁰+

15. 如图，二次函数的图象开口向上,图像经过点(-1，2)和(1，0)且与y轴交于负半轴．

(以下有(1)、(2)两问，每个考生只须选答一问，若两问都答，则只

　以第(2)问计分)

　第(1)问：给出四个结论：①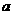＞0；②＞0；③＞0； ④a+b+c=0

　　　　其中正确的结论的序号是　 ▲　 (答对得3分，少选、错选

　　　　均不得分)．

　第(2)问：给出四个结论：①abc＜0；②2a+＞0；③a+c=1；

　　　　④a＞1．其中正确的结论的序号是　 ▲　 (答对得5分，少选、错选均不得分)．

○16. 已知一列数：1，―2，3，―4，5，―6，7，…　将这列数排成下列形式：

第1行　　 1

第2行　 －2　　　 3

第3行　 －4　　　 5　　 －6

第4行　　 7　　 －8　　 　9　　 －10

第5行　　 11　　 －12　　　 13　　 －14　　 15

…　　　　 …

按照上述规律排下去，那么第10行从左边数第5个数等于　　　 ．

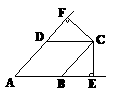
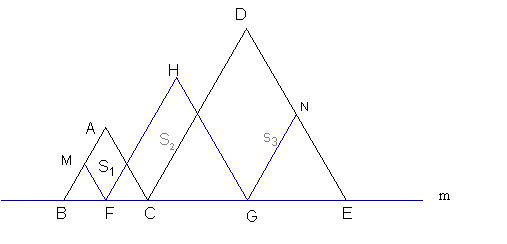☆16. 如图，在直线m上摆故着三个正三角形:△ABC、△HFG、△DCE,已知BC=CE,F、G分别是BC、CE的中点，FM∥AC，GN∥DC．设图中三个平行四边形的面积依次是S₁,S₂,S₃,若S₁+S₃=10，则S₂=　　　 .

14.日常生活中，“老人”是一个模糊概念．有人想用“老人系数”来表示一个人的老年化程度．他设想“老人系数”的计算方法如下表：

人的年龄x(岁)	x≤60	60＜x＜80	x≥80
该人的“老人系数”	0		1

按照这样的规定，一个70岁的人的“老人系数”为　　　　　　 ．