5.正多边形的外接圆(或内切圆)的圆心叫正多边形的中心.外接圆半径叫正多边形的半径.内切圆的半径叫正多边形的边心距.正多边形的每一边所对的圆心角叫中心角,中心角的度数是.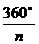

如图:OA,OB是半径,O是中心,

OH⊥AB于H,OH是边心距,

是中心角.　　　　　　　　　　　　　　　　 O

　　　　　　　　　　　　　　　　　 A　　 H　　 B

4.正多边形的性质:任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆.

3.正多边都是轴对称图形,若n是奇数,正n边形是轴对称图形,n是偶数,正n边形既是轴对称图形又是中心图形.

2.正多边形的判定,正多边形的定义当然是正多边形的判定方法之一,但如同全等三角形的判定一样,用定义来证明两个三角形全等显然不可取,因此需用判定定理来证.

判定定理:把圆几等分()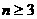

①依次连结各分点所得的多边形是这个圆的内接正边形

②经过各分点做圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正边形.也就是说,若要证明一个多边形是圆内接正多边形,只要证明这个多边形的顶点是圆的等分点即可, 如：要证明一个圆内接边形ABCDEF……是圆内接正边形,就要证A、B、C、D、E、F……各点是圆的n等分点,就是要证AB=BC=CD=DE=EF=…….同样,要证明一个圆外切边形是圆外切正边形,只要证明各切点是圆的等分点即可.

例1:证明：各边相等的圆内接多边形是正多边形.

已知:在⊙O中,多边形ABCDE……

　　 是⊙O的内接n边形,　　　　　　　　　　 O　　　　 　　E

　　　　 且AB=BC=CD=DE=…….　　

求证:n边形ABCDE……是正n边形.　　　　　　 A　　　　　　　 D

证明: AB=BC=CD=DE=……　　　　　　　　　　　　　 B　　　 C

　　　 ∴ AB=BC=CD=DE……

　　　 ∴OEB=AEC= BED=COE=……

　　　 ∴

　　 又∵AB=BC=CD=DE=……　　

　　　 ∴n边形ABCDE……是正n边形.

例2:证明:各角相等的圆外切n边形是正n边形.

已知:多边形……是圆外切n边形,切点分别是A,B,C,D,E……,=…….

求证:n边形……是正n边形.

证明:连结OB,OC,OD……,在四边形COD和四边形BOC中

　　 ∵切⊙O于B,C,D

　　 ∴

　　 ∴ 　　　　　A　　　　 F　

　　 而……　　　　　　　 　　　　　　　

　　 ∴

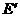
　　 ∴BC=CD(在同圆中,相等的圆　　　　　　 B　　　　 O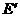　　

　　　 心角所对的弧相等).　　　　　　　　　　　　　　　　　

　　 同理BC=CD=DE=FE=……　　　　　　　 　　　　　　　　D

　　 ∴A,B,C,D,E,F……是圆的n等分点　　　　　 C

　　 ∴多边形ABCDEF……是圆外切n正多边形　　　　　

1.正多边形的定义:各边相等、各角也相等的多边形叫做正多边形.此定义中的条件各边相等,各角也相等 “缺一不可”.如:菱形各边相等,因四个角不等,所以菱形不一定是正多边形.矩形的四个角相等,但因四条边不一定相等,故矩形不一定是正四边形,只有正方形是正四边形.

24. (本小题满分12分)

OABC是一张放在平面直角坐标系中的矩形纸片，O为原点，点A在x轴上，点C在y轴上，OA=10，OC=6.

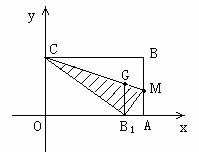(1)如图，在AB上取一点M，使得△CBM沿CM翻折后，点B落在x轴上，记作B₁点，求B₁点的坐标；

(2) 求折痕CM所在直线的解析式；

(3) 作B₁G∥AB交CM与点G，若以C为顶点的抛物线过点G，求此抛物线的解析式.

23. (本小题满分12分)

某厂生产流水线要招聘操作工和包装工150人，操作工和包装工的月基本工资分别为1000元和600元，(1)现要求操作工的人数不少于包装工人数的2倍，问：操作工和包装工各招聘多少人时，可使每月所付的基本工资总额最小，最小值是多少？(2)在上述招聘两类员工月基本工资总额最小的条件下，工厂另增加10万元奖金，其中包装工奖金不大于操作工的奖金，但不低于200元，若以百元为单位发放奖金，问：有几种奖励方案？把它们都写出来.

22. (本小题满分8分)

在平面直角坐标系中，A点坐标为(0，4)，C点坐标为(10，0)，

(1) 如图1，若直线AB∥OC，AB上有一动点P，当PO=PC时，求P点的坐标；

(2) 如图2，若直线AB与OC不平行，AB所在直线y=－x+4上是否存在点P，

使∠OPC=90°，若有这样的点P，求出它的坐标，若没有，请简要说明理由.

21. (本小题满分8分)

如图，已知□ABCD中，E为AD的中点，CE的延长线交BA的延长线于点F，

(1) 求证：CD=FA；

(2) 若使∠F=∠BCF，□ABCD的边长之间还需要加一个什么条件？请你补上这个条件，并证明.(不要再添辅助线)

20. (本小题满分8分)

如图，平面直角坐标系中，△ABC是边长为3的正三角形，其中点B的坐标为(－4，1)，点C的坐标为(－1，1)，请按下列要求进行操作和探索：

(1)以y轴为对称轴作△ABC的对称图形△A₁B₁C₁,(不写作法,保留作图痕迹)；

(2)以x轴为对称轴作△A₁B₁C₁的对称图形△A₂B₂C₂,(不写作法,保留作图痕迹)；

(3)直接写出点B₁ 、A₂的坐标；

(4)探索：能否通过一次旋转将△ABC旋转到△A₂B₂C₂的位置？你若认为能，请作出肯定回答，并指出这时的旋转中心和旋转的角度；你若认为不能，请作出否定回答(不必说明理由).