3、将一张矩形白纸对折，再沿着与折痕方向平行的方向反复对折，问经过n(1≤n≤7)次后，将纸展开共可得到的折痕条数为(　 )

　 A、2 ⁿ －1 B．2 ⁿ　 C、 2 ^n-1　 D．2 n

2．小亮同学想在房子附近开辟一块绿化场地，现共有。米长的篱笆材料，他设计了两种方案，一种是围成正方形的场地，另一种是围成圆形的场地，那么选用哪一种方案围成场地的面积较大(　 )

　 A、围成正方形　　　 B．围成圆形　　 C、两者一样大　　　 D．不能确定

1．某研究结果显示，由父母的身高预测子女身高的公式为：若父亲的身高为a米，母亲的身高为b米，则儿子成年后的身高约为×1．08米，女儿成年后身高约为米，初一女学生赵楠的父亲身高为1．75米，母亲身高为1．62米，请同学们根据公式预测一下赵楠成年后的身高约为(　 )

　　 A．1．65米　　 　　　B．1．62米　　 C．1．7 5米　　　　　 D．l．6 0米

3．(10分)如图2－7－4所示，甲、乙两辆大型货车于下午2：00同时从A地出发驶往P市，甲车沿一条公路向北偏东60^o方向行驶，直达P市，其速度为30千米/时；乙车先沿一条公路向正东方向行驶半小时后到达B地，卸下部分货物，再沿一条通向东北方向的公路驶往P市，其速度始终为40千米/时．

⑴ 设出发后经过t小时，甲车与P市的距离为s千米,求s与t之间的函数表达式，并写出自变量t的取值范围．

⑵ 已知在P市新建的移动通讯接收发射塔，其信号覆盖面积只可达P市周围方圆30千米的区域(包括边缘地带人除此之外，该地区无其他发射塔．故甲、乙两车司机只能靠P市发射塔进行手机通话联系，问甲、乙两车司机从什么时刻开始可取得联系(精确到分钟)

2．(10分)如图2－7－3所示，这些等腰三角形与正三角形的形状有差异，我们把它与正三角形的接近程度称为“正度”，在研究“正度”时，应保证相似三角形的“正度”相等．设等腰三角形的底和腰分别为儿为，底角和顶角分别为以尽要求“正度”的值是非负数．同学甲认为：可用式子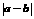来表示“正度”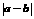，的值越小，表示等腰三角形越接近正三角形；同学乙认为：可用式子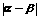来表示“正度”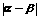，的值越小，表示等腰三角形越接近正三角形．

　 探究：

⑴ 他们的方案哪个较为合理，为什么？

⑵ 对你认为不够合理的方案，请加以改进(给出式子即可)

⑶ 请再给出一种衡量“正度”的表达式．

5、(2005年泰州)图1是边长分别为4和3的两个等边三角形纸片ABC和C′D′E′叠放在一起(C与C′重合).

(1)操作：固定△ABC，将△C′D′E′绕点C顺时针旋转30°得到△CDE，连结AD、BE，CE的延长线交AB于F(图2)；

探究：在图2中，线段BE与AD之间有怎样的大小关系？试证明你的结论.(4分)

(2)操作：将图2中的△CDE，在线段CF上沿着CF方向以每秒1个单位的速度平移，平移后的△CDE设为△PQR(图3)；

探究：设△PQR移动的时间为x秒，△PQR与△ABC重叠部分的面积为y，求y与x之间的函数解析式，并写出函数自变量x的取值范围.

(3)操作：图1中△C′D′E′固定，将△ABC移动，使顶点C落在C′E′的中点，边BC交D′E′于点M，边AC交D′C′于点N，设∠AC C′=α(30°＜α＜90°＝(图4)；

探究：在图4中，线段C′N·E′M的值是否随α的变化而变化？如果没有变化，请你求出C′N·E′M的值，如果有变化，请你说明理由.

4、(2005年枣庄)如图甲，四边形ABCD是等腰梯形，AB∥DC．由4个这样的等腰梯形可以拼出图乙所示的平行四边形.

(1)求四边形ABCD四个内角的度数；

(2)试探究四边形ABCD四条边之间存在的等量关系，并说明理由；

　 (3)现有图甲中的等腰梯形若干个，利用它们你能拼出一个菱形吗?若能，请你画出大致的示意图．