12.如图，已知抛物线的顶点坐标为M(1,4)，且经过点N(2,3)，与x轴交于A、B两点(点A在点B左侧)，与y轴交于点C。

(1)求抛物线的解析式及点A、B、C的坐标；

(2)若直线y=kx+t经过C、M两点，且与x轴交于点D，试证明四边形CDAN是平行四边形；

(3)点P在抛物线的对称轴x=1上运动，请探索：在x轴上方是否存在这样的P点，使以P为圆心的圆经过A、B两点，并且与直线CD相切，若存在，请求出点P的坐标；若不存在，请说明理由。

11.如图，在Rt△ABC中，已知AB＝BC＝CA＝4cm，AD⊥BC于D，点P、Q分

别从B、C两点同时出发，其中点P沿BC向终点C运动，速度为1cm/s；点P沿CA、AB向终点B运动，速度为2cm/s，设它们运动的时间为x(s)。

⑴ 求x为何值时，PQ⊥AC；

⑵ 设△PQD的面积为y(cm²)，当0＜x＜2时，求y与x的函数关系式；

⑶ 当0＜x＜2时，求证：AD平分△PQD的面积；

⑷ 探索以PQ为直径的圆与AC的位置关系。请写出相应位置关系的x的取值范围(不要求写出过程)

10.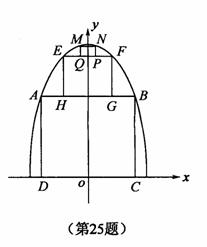为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为,正方形ABCD的边长和正方形EFGH的边长之比为5∶1,求：

(1)抛物线解析式中常数的值;

(2)正方形MNPQ的边长.

9.已知二次函数的图象过点M(0，-3)，并与x轴交于点A(x₁，0)、B(x₂，0)两点，且x₁²+x₂²＝10。试求这个二次函数的解析式。

8．教师提出：如图A(1,0)，AB＝OA，过点A、B作x轴的垂线交二次函数的图象于C、D两点，直线OC交BD于点M，直线CD交y轴于点H，记点C、D的横坐标分别为，点H的纵坐标为。

同学讨论发现：①2 ：3　 ②

⑴ 请你验证①②结论成立；

⑵ 请你研究：如将上述条件“A(1，0)”改为“A”，其他条件不娈，结论①是否仍成立？

⑶ 进一步研究：在⑵的条件下，又将条件“”改为“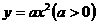，其他条件不娈，那么和有怎样的数值关系？(写出结果并说明理由)

7.]已知：如图，抛物线关于轴对称；抛物线关于y轴对称。抛物线与x轴相交于A、B、C、D四点；与y相交于E、F两点；H、G、M分别为抛物线的顶点。HN垂直于x轴，垂足为N，且

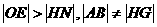
(1)A、B、C、D、E、F、G、H、M9个点中，四个点可以连接成一个四边形，请你用字母写出下列特殊四边形：菱形　　　　　　 ；等腰梯形　　　　　 ；平行四边形　　　　　 ；梯形　　　　　　 ；(每种特殊四边形只能写一个，写错、多写记0分)

(2)证明其中任意一个特殊四边形；

(3)写出你证明的特殊四边形的性质。

6.农民张大伯为了致富奔小康，大力发展家庭养殖业。他准备用40m长的木栏围一个矩形的羊圈，为了节约材料同时要使矩形的面积最大，他利用了自家房屋一面长25m的墙，设计了如图一个矩形的羊圈。

(1)请你求出张大伯矩形羊圈的面积；

(2)请你判断他的设计方案是否合理？如果合理，直接答合理；如果不合理又该如何设计？并说明理由。

5.如图，用长为18 m的篱笆(虚线部分)，两面靠墙围成矩形的苗圃.

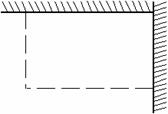(1)设矩形的一边为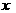(m)，面积为(m²)，求关

于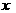的函数关系式，并写出自变量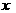的取值范围；

(2)当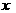为何值时，所围苗圃的面积最大，最大面积是多少？

4.[05丽水]某校的围墙上端由一段段相同的凹曲拱形栅栏组成，如图所示，其拱形图形为抛物线的一部分，栅栏的跨径AB间，按相同的间距0.2米用5根立柱加固，拱高OC为0.6米．

(1) 以O为原点，OC所在的直线为y轴

建立平面直角坐标系，请根据以上的数据，求出抛物线y=ax²的解析式；

(2)计算一段栅栏所需立柱的总长度．(精确到0.1米)

3.[05嘉兴]在坐标平面内，半径为R的⊙O与x轴交于点D(1，0)、E(5，0)，与

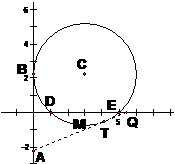y轴的正半轴相切于点B。点A、B关于x轴对称，点P(a，0)在x的正半轴上运动，作直线AP，作EH⊥AP于H。

(1)　　　 求圆心C的坐标及半径R的值；

(2)　　　 △POA和△PHE随点P的运动而变化，若它们全等，求a的值；

(3)　　　 若给定a=6，试判定直线AP与⊙C的位置关系(要求说明理由)。