27．汽车从A 地开往B 地，如果在原计划时间的前一半时间每小时驶40千米，而后一半时间由每小时行驶50千米，可按时到达．但汽车以每小时40千米的速度行至离AB 中点还差40千米时发生故障，停车半小时后，又以每小时55千米的速度前进，结果仍按时到达B 地．求AB 两地的距离及原计划行驶的时间．

[提示]设原计划用x 小时，AB 两地距离的一半为y 千米，

根据题意，得

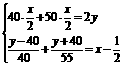
[答案]x＝8，2y＝360．

[点评] 与本例中设AB 两地距离的一半为y 千米一样，也可设原计划的一半时间为x 小时．恰当地设未知数，可以使列方程组和解方程组都更加简便．

26．某人买了4 000元融资券，一种是一年期，年利率为9%，另一种是两年期，年利率是12%，分别在一年和两年到期时取出，共得利息780元．两种融资券各买了多少？

[提示]若设一年期、二年期的融资券各买x 元，y 元，

由题意，得

[答案]x＝1 200，y＝2 800．

[点评]本题列方程组时，易将二年期的融资券的利息误认为是y元，应弄清题设给出的是年利率，故几年到期的利息应该乘几．

25．有一个三位整数，将左边的数字移到右边，则比原来的数小45；又知百位上的数的9倍比由十位上的数与个位上的数组成的两位数小3．求原来的数．

[提示]设百位上的数为x，由十位上的数与个位上的数组成的两位数为y，

根据题意，得

[答案]x＝4，y＝39，三位数是439．

[点评]本例分别设十位上的数和个位上的数为不同的未知数，无论从列方程组还是解方程组都更加简捷易行．

24．当x＝1，3，－2时，代数式ax²+bx+c 的值分别为2，0，20，求：(1)a、b、c 的值；(2)当x＝－2时，ax²+bx+c 的值．

[提示]由题得关于a、b、c 的三元一次方程组，求出a、b、c 再代入这个代数式．

[答案]a＝1，b＝－5，c＝6；20．

[点评]本例若不设第一问，原则上也应在求出a、b、c 后先写出这个代数式，再利用它求值．用待定系数法求a、b、c ，是解这类问题常用的方法．

23．已知满足方程2 x－3 y＝m－4与3 x+4 y＝m+5的x，y也满足方程2x+3y＝3m－8，求m 的值．

[提示]由题意可先解方程组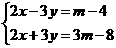用m 的代数式表示x，y

再代入3 x+4 y＝m+5．

[答案]m＝5．

22．甲、乙两人解方程组，甲因看错a，解得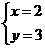，乙将其中一个方程的b 写成了它的相反数，解得，求a、b 的值．

[提示]可从题意的反面入手，即没看错什么入手．如甲看错a，即没看错b，所求得的解应满足4 x－by＝－1；而乙写错了一个方程中的b，则要分析才能确定，经判断是将第二方程中的b 写错．

[答案]a＝1，b＝3．

21．已知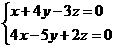，xyz ≠0，求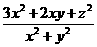的值．

[提示]把z看作已知数，用z的代数式表示x、y，可求得x∶y∶z＝1∶2∶3．设x＝k，

y＝2 k，z＝3 k，代入代数式．

[答案]．

[点评]本题考查了方程组解法的灵活运用及比例的性质．若采用分别消去三个元可得方程21 y－14 z＝0，21 x－7 z＝0，14 x－7 y＝0，仍不能由此求得x、y、z的确定解，因为这三个方程不是互相独立的．

20．[提示] 将三个方程左，右两边分别相加，得4x－4y+4z＝8，故 x－y+z＝2　 ④，把④分别与第一、二个方程联立，然后用加、减消元法即可求得x、z 的值．[答案]

19．

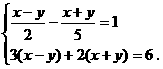
[提示]用换元法，设x－y＝A，x+y＝B，解关于A、B 的方程组，

进而求得x，y．[答案]

18．

[提示]将方程组化为整系数方程的一般形式，再用加减法消元．

[答案]