
题目列表(包括答案和解析)
23.某旅游胜地欲开发一座景观山.从山的侧面进行堪测,迎面山坡线ABC由同一平面内的两段抛物线组成,其中AB所在的抛物线以A为顶点、开口向下,BC所在的抛物线以C为顶点、开口向上.以过山脚(点C)的水平线为x轴、过山顶(点A)的铅垂线为y轴建立平面直角坐标系如图(单位:百米)。已知AB所在抛物线的解析式为 ,BC所在抛物线的解析式为
,BC所在抛物线的解析式为 ,且已知
,且已知 。
。
(1)设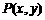 是山坡线AB上任意一点,用y表示x,并求点B的坐标;
是山坡线AB上任意一点,用y表示x,并求点B的坐标;
(2)从山顶开始、沿迎面山坡往山下铺设观景台阶。这种台阶每级的高度为20厘米,长度因坡度的大小而定,但不得小于20厘米,每级台阶的两端点在坡面上(见图)。
①分别求出前三级台阶的长度(精确到厘米);
②这种台阶不能一直铺到山脚,为什么?
 (3)在山坡上的700米高度(点D)处恰好有一小块平地,可以用来建造索道站.索道的起点选择在山脚水平线上的点E处,
(3)在山坡上的700米高度(点D)处恰好有一小块平地,可以用来建造索道站.索道的起点选择在山脚水平线上的点E处,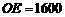 (米)。假设索道DE可近似地看成一段以E为顶点、开口向上的抛物线,解析式为
(米)。假设索道DE可近似地看成一段以E为顶点、开口向上的抛物线,解析式为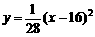 。试求索道的最大悬空高度。
。试求索道的最大悬空高度。
22.如图,已知△ABC, ,
, .O是AB的中点,⊙O与AC相切于点D、与BC相切于点E。设⊙O 交OB于F,连DF并延长交CB的延长线于G。
.O是AB的中点,⊙O与AC相切于点D、与BC相切于点E。设⊙O 交OB于F,连DF并延长交CB的延长线于G。
 (1)
(1) 与
与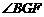 是否相等?为什么?
是否相等?为什么?
(2)求由DG、GE和弧ED所围成图形的面积(阴影部分)。
21.马戏团让狮子和公鸡表演跷跷板节目。跷跷板支柱AB的高度为1.2米。
(1)若吊环高度为2米,支点A为跷跷板PQ的中点,狮子能否将公鸡送到吊环上?为什么?
 (2)若吊环高度为3.6米,在不改变其他条件的前提下移动支柱,当支点A移到跷跷板PQ的什么位置时,狮子刚好能将公鸡送到吊环上?
(2)若吊环高度为3.6米,在不改变其他条件的前提下移动支柱,当支点A移到跷跷板PQ的什么位置时,狮子刚好能将公鸡送到吊环上?
20. 已知一次函数的图象经过
已知一次函数的图象经过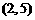 和
和 两点.
两点.
(1)在给定坐标系中画出这个函数的图象;
(2)求这个一次函数的解析式。
19.如图,已知∠1=∠2,∠C=∠D,求证:AC=BD.

18.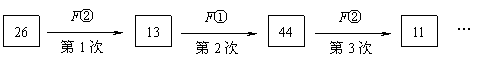 定义一种对正整数n的“F运算”:①当n为奇数时,结果为
定义一种对正整数n的“F运算”:①当n为奇数时,结果为 ;②当n为偶数时,结果为
;②当n为偶数时,结果为 (其中k是使
(其中k是使 为奇数的正整数),并且运算重复进行.例如,取
为奇数的正整数),并且运算重复进行.例如,取 ,则:
,则:
若 ,则第449次“F运算”的结果是多少?
,则第449次“F运算”的结果是多少?
17.如图,矩形纸片ABCD,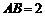 ,
, ,
,
沿对角线BD折叠(使△ABD和△EBD落在同一
平面内),则A、E两点间的距离为多少?
16.计算: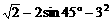 .
.

15.解不等式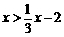 ,并将其解集表示在数轴上.
,并将其解集表示在数轴上.

14.如图,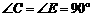 ,
, ,
, ,
,
 ,则
,则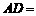 _________。
_________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com