
题目列表(包括答案和解析)
(1)分别求点E, C的坐标.
(2)求经过A、C两点,且以过E而平行于y轴的直线为对称轴的抛物线的函数解析式.
 (3)设抛物线的对称轴与AC的交点为M,试判断以M点为圆心, ME为半径的圆与☉A的位置关系,并说明理由.
(3)设抛物线的对称轴与AC的交点为M,试判断以M点为圆心, ME为半径的圆与☉A的位置关系,并说明理由.
一个圆柱的一条母线为AB,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的表面爬行到点C.
⑴如图①,如果底面周长为24cm,高为4cm,那么蚂蚁的最短行程是多少cm?
⑵如图②,如果底面半径为rcm,高为hcm,那么你认为蚂蚁可能有哪几种行程较短的路径?试画出平面展开图说明路径(至少画两种不同的路径),不必说明理由.
⑶通过计算比较②中各种路径的长度,你能得到什么一般性的结论?或者说,蚂蚁选择哪条路径可使行程最短?

28、(12分)某企业有员工300人,生产A种产品,平均每人每年可创造利润 万元(
万元( 为大于零的常数)。为减员增效,决定从中调配
为大于零的常数)。为减员增效,决定从中调配 人去生产新开发的B种产品,根据评估,调配后,继续生产A种产品的员工平均每人每年创造的利润可增加20%,生产B种产品的员工平均每人每年可创造利润1.54
人去生产新开发的B种产品,根据评估,调配后,继续生产A种产品的员工平均每人每年创造的利润可增加20%,生产B种产品的员工平均每人每年可创造利润1.54 万元。
万元。
(1)调配后,企业生产A种产品的年利润为_________万元,企业生产B种产品的年利润为_________万元(用含 和
和 的代数式表示)。若设调配后企业全年总利润为
的代数式表示)。若设调配后企业全年总利润为 万元,则
万元,则 与
与 之间的关系式为
之间的关系式为 =____________。
=____________。
(2)若要求调配后,企业生产A种产品的年利润不小于调配前企业年利润的 ,生产B种产品的年利润大于调配前企业年利润的一半,应有哪几种调配方案
?请设计出来,并指出其中哪种方案全年总利润最大(必要时,运算过程可保留3个有效数字)。
,生产B种产品的年利润大于调配前企业年利润的一半,应有哪几种调配方案
?请设计出来,并指出其中哪种方案全年总利润最大(必要时,运算过程可保留3个有效数字)。
(3)企业决定将(2)中的年最大总利润(设 =2)继续投资开发新产品。现有6种产品可供选择(不得重复投资同一种产品)各产品所需资金及所获年利润如下表:
=2)继续投资开发新产品。现有6种产品可供选择(不得重复投资同一种产品)各产品所需资金及所获年利润如下表:
|
产
品 |
C |
D |
E |
F |
G |
H |
|
所需资金(万元) |
200 |
348 |
240 |
288 |
240 |
500 |
|
年 利 润(万元) |
50 |
80 |
20 |
60 |
40 |
85 |
如果你是企业决策者,为使此项投资所获年利润不少于145万元,你可以投资开发哪些产品?请写出两种投资方案。
31.(本小题12分)
如图,梯形OABC中,BC∥AO,∠BAO=90°,B(-3 ,3),直线OC的解析式为
,3),直线OC的解析式为
y=- x,将ΔOBC绕点C顺时针旋转60°后,O到O1,B到B1,得ΔO1B1C.
x,将ΔOBC绕点C顺时针旋转60°后,O到O1,B到B1,得ΔO1B1C.
(1)求证:点O1在x轴上;
(2)将点O1运动到点M(-4 ,0),求∠B1MC的度数;
,0),求∠B1MC的度数;
(3)在(2)的条件下,将直线MC向下平移m个单位长度,设直线MC与线段AB交于点P,与线段OC的交于点Q,四边形OAPQ的面积为S,求S与m的函数关系式,并求出m的取值范围.

解:(1)由题意:C(- ,3)
,3)
∴tan∠COA=
∴∠COA=60°
∵∠OCO1=60°,CO=CO1
∴ΔCOO1为等边三角形
∴∠COO1=60°
∴∠COA=∠COO1
∴点O1在x轴上. ……4’
∵∠COO1=60°,BC∥AO
(2)∠BCO=120°
∴BCO1=120°
∵∠O1CO=60°
∴∠BCO=180°
∴B、C、O三点共线
∴C(- ,3)
,3)
∴CO=CO1=O1O=2
∵M1O=4
∴M1O1=O1O=O1C
可证得 ∠M1CO=90°
∵BC=CO=2
BC=B1C
∴B1C=CO
∴M1B=M1O
∴∠BM1C= ∠B1M1O=30° ……8’
∠B1M1O=30° ……8’
(2) ∵AD=1,PD=m
∴AP=1-m
在ΔCEQ中,CE=m,∠ECQ=30°
∴CQ= m
m
∴OQ=2 -
- m
m
∴QN=3- m,ON=
m,ON= -
- m
m
∴AN=2 +
+ m
m
又∵S四边形OAPQ=S梯形PAQN+SΔQNO
∴S= [(1―m)+(3―
[(1―m)+(3― m)][2
m)][2 +
+ m]+
m]+ (
( ―
― m)(3―
m)(3― m)
m)
∴S=― m2―2
m2―2 m+
m+
 (0<m<1) ……12’
(0<m<1) ……12’
28.(1)B(6,0)………………………………4分
(2) ………………………………8分
………………………………8分
(3)存在。N(-3,0)………………………………12分
24.解. (1)OA=OB,DF=EF,DE=AC,AG=DG,EG=CG. ………………………………3分
(2)ME=GM. 理由是:连EO并延长交⊙O于点N,连结DN.
∵EM是⊙O的切线,
∴∠OEM=90º,∴∠GEM+∠GEN=90º. …………………………………………5分
∵EN是⊙O的直径,∠N+∠GEN=90º,
∴∠N=∠GEM. ………………………………………………………………7分
∵AB是⊙O的直径,∴∠B+∠BAC=90º,
∵∠AGF+∠GAF=90º,∴∠AGF=∠B,……………………………………9分
∵∠AGF=∠CGE,∴∠CGE=∠B.
∵AC=DE,∴∠N=∠B,
∴∠GEM=∠CGE,∴MG=ME. ………………………………………………11分
(3)答案: .…………………………………………………………………14分
.…………………………………………………………………14分
28(本题满分12分)
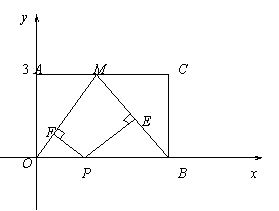
如图:矩形的顶点在坐标原点O,OA在y轴上,A点坐标为(0,3),另一边OB在x的正半轴上,点M是AC边的中点,点P是OB边上一动点,PF⊥OM,PE⊥BM,垂足分别为E、F.
(1)若四边形PEMF为矩形,求B点坐标;
(2)在(1)的条件下,求过A、M、B三点的抛物线解析式;
(3)在抛物线上是否存在一点N,使得四边形AMON是平行四边形,若存在,求出点N的坐标,若不存在,说明理由。
24.  如图,已知AB是⊙O的直径,AC是⊙O的弦,点D是弧ABC中点,弦DE⊥AB,垂足为F,DE交AC于点G.
如图,已知AB是⊙O的直径,AC是⊙O的弦,点D是弧ABC中点,弦DE⊥AB,垂足为F,DE交AC于点G.
(1)图中有哪些相等的线段?(要求:不再标注其他字母,找结论的过程中所作的辅助线不能出现在结论中,不写出推理过程)
(2)若过点E作⊙O的切线ME,交AC的延长线于点M(请补完整图形),试问:ME=MG是否成立?若成立,请证明;若不成立,请说明理由.
(3)在满足第(2)问的条件下,已知AF=3,FB= ,求AG与GM的比.[第(1)的结论可直接利用]
,求AG与GM的比.[第(1)的结论可直接利用]
17、(本小题满分10分)
解:(1)设点P的坐标为 ,则
,则
 PM=
PM= ;
;
又因为点P到直线 的距离为
的距离为 ,
,
所以,以点P为圆心,PM为半径的圆与直线 相切.
(得4分)
相切.
(得4分)
(2)如图,分别过点P,Q作直线 的垂线,垂足分别为H,R.由(1)知,PH=PM,同理可得,QM=QR.
的垂线,垂足分别为H,R.由(1)知,PH=PM,同理可得,QM=QR.
因为PH,MN,QR都垂直于直线 ,所以,PH∥MN∥QR,于是
,所以,PH∥MN∥QR,于是
 ,
,
所以
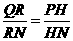 ,
,
因此,Rt△ ∽Rt△
∽Rt△ .
.
于是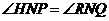 ,从而
,从而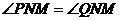 (得6分)
(得6分)
17.(本小题满分10分).已知点M,N的坐标分别为(0,1),(0,-1),点P是抛物线 上的一个动点.(1)求证:以点P为圆心,PM为半径的圆与直线
上的一个动点.(1)求证:以点P为圆心,PM为半径的圆与直线 的相切;
的相切;
(2)设直线PM与抛物线 的另一个交点为点Q,连接NP,NQ,求证:
的另一个交点为点Q,连接NP,NQ,求证: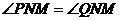 .
.

24.(1)t= (3分)
(3分)
(2)OC=CP (4分)
过点C作X轴的平行线,交OA与直线BP于点T、H,
证△OTC≌△CHP即可 (7分)
(3)① (0≤t≤1)
(10分)
(0≤t≤1)
(10分)
②当t=0或1时,△PBC为等腰三角形,
即P(1.1), P(1,1- ) (12分 )
) (12分 )
24.如图,点A在Y轴上,点B在X轴上,且OA=OB=1,经过原点O的直线L交线段AB于点C,过C作OC的垂线,与直线X=1相交于点P,现将直线L绕O点旋转,使交点C从A向B运动,但C点必须在第一象限内,并记AC的长为t,分析此图后,对下列问题作出探究:
(1)当△AOC和△BCP全等时,求出t的值。
(2)通过动手测量线段OC和CP的长来判断它们之间的大小关系?并证明你得到的结论。
 (3)①设点P的坐标为(1,b),试写出b关于t的函数关系式和变量t的取值范围。②求出当△PBC为等腰三角形时点P的坐标。
(3)①设点P的坐标为(1,b),试写出b关于t的函数关系式和变量t的取值范围。②求出当△PBC为等腰三角形时点P的坐标。
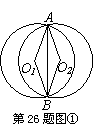
24.(本题满分12分)
如图①、②、③是两个半径都等于2的⊙O1和⊙O2,由重合状态沿水平方向运动到互相外切过程中的三个位置,⊙O1和⊙O2相交于A、B两点,分别连结O1A、O1B、O2A、O2B和AB。
(1)如图②,当∠AO1B=120°时,求两圆重叠部分图形的周长l;(4分)
(2)设∠AO1B的度数为x,两圆重叠部分图形的周长为y,求y关于x的函数关系式,并写出自变量x的取值范围;(4分)
(3)由(2),若y=2x,则线段O2A所在的直线与⊙O1有何位置关系?为什么?除此之外,它们还有其它的位置关系,写出其它位置关系时x的取值范围。(4分)



湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com