(二)图形与变换

　 　⒈图形的轴对称、图形的平移、图形的旋转。

　 　考试内容：

　 　轴对称、平移、旋转。

　 　考试要求：

　 (1)通过具体实例认识轴对称(或平移、旋转)，探索它们的基本性质；

　 (2)能够按要求作出简单平面图形经过轴对称(或平移、旋转)后的图形，能作出简单平面图形经过一次或两次轴对称后的图形；

　 (3)探索基本图形(等腰三角形、矩形、菱形、等腰梯形、正多边形、圆)的轴对称(或平移、旋转)的性质及其相关性质。

　 (4)利用轴对称(或平移、旋转)及其组合进行图案设计；认识和欣赏轴对称(或平移、旋转)在现实生活中的应用。

　 　⒉图形的相似

　 　考试内容：

　 　比例的基本性质，线段的比，成比例线段，图形的相似及性质，三角形相似的条件，图形的位似，锐角三角函数，30、45、60角的三角函数值。

　 　考试要求：

　 (1)了解比例的基本性质，了解线段的比、成比例线段，通过实例了解黄金分割。

　 (2)通过实例认识图形的相似，了解相似图形的性质，知道相似多边形的对应角相等，对应边成比例，面积的比等于对应边比的平方。

　 (3)了解两个三角形相似的概念，掌握两个三角形相似的条件。

　 (4)了解图形的位似，能够利用位似将一个图形放大或缩小。

　 (5)通过实例了解物体的相似，利用图形的相似解决一些实际问题(如利用相似测量旗杆的高度)。

　 (6)通过实例认识锐角三角函数(sinA，cosA， tanA)，知道30、45、60角的三角函数值；会使用计算器由已知锐角求它的三角函数值，由已知三角函数值求它对应的锐角。

　 (7)运用三角函数解决与直角三角形有关的简单实际问题。

(一)图形的认识

　 ⒈点、线、面，角。

　 　考试内容：

　 　点、线、面、角、角平分线及其性质。

　 　考试要求：

　 　(1)在实际背景中认识，理解点、线、面、角的概念。

　 (2)会比较角的大小，能估计一个角的大小，会计算角度的和与差，认识度、分、秒，会进行简单换算。

　 (3)掌握角平分线性质定理及逆定理。

　 　⒉相交线与平行线

　 　考试内容：

　 　补角，余角，对顶角，垂线，点到直线的距离，线段垂直平分线及其性质，平行线，平行线之间的距离，两直线平行的判定及性质。

　 　考试要求：

　 　(1)了解补角、余角、对顶角的概念，知道等角的余角相等、等角的补角相等、对顶角相等。

　 (2)了解垂线、垂线段等概念，会用三角尺或量角器过一点画一条直线的垂线。了解垂线段最短的性质，理解点到直线距离的意义。

　 　(3)知道过一点有且仅有一条直线垂直于已知直线。

　 (4)掌握线段垂直平分线性质定理及逆定理。

　 (5)了解平行线的概念及平行线基本性质，

　 (6)掌握两直线平行的判定及性质。

　 (7)会用三角尺和直尺过已知直线外一点画这条直线的平行线。

　 (8)体会两条平行线之间距离的意义，会度量两条平行线之间的距离。

　 　⒊三角形

　 　考试内容：

　 　三角形，三角形的角平分线、中线和高，三角形中位线，全等三角形、全等三角形的判定，等腰三角形的性质及判定。等边三角形的性质。直角三角形的性质及判定。勾股定理。勾股定理的逆定理。

　 　考试要求：

(1)了解三角形有关概念(内角、外角、中线、高、角平分线)，会画出任意三角形的角平分线、中线和高。

　 (2)掌握三角形中位线定理。

　(3)了解全等三角形的概念，掌握两个三角形全等的判定定理。

　 (4)了解等腰三角形、直角三角形、等边三角形的有关概念，掌握等腰三角形、直角三角形、等边三角形的性质和判定定理；

　 (5)掌握勾股定理，会运用勾股定理解决简单问题；会用勾股定理的逆定理判定直角三角形。

　 　⒋四边形

　 　考试内容：

　 　多边形，多边形的内角和与外角和，正多边形，平行四边形、矩形、菱形、正方形、梯形的概念和性质，平面图形的镶嵌。

　 　考试要求：

　 　(1)了解多边形的内角和与外角和公式，了解正多边形的概念。

　 　(2)掌握平行四边形、矩形、菱形、正方形、梯形的概念和性质，了解它们之间的关系；了解四边形的不稳定性。

　 　(3)掌握平行四边形、矩形、菱形、正方形、等腰梯形的有关性质和判定定理。

　 　(4)了解线段、矩形、平行四边形、三角形的重心及物理意义(如一根均匀木棒、一块均匀的矩形木板的重心)。

　 (5)通过探索平面图形的镶嵌，知道任意一个三角形、四边形或正六边形可以镶嵌平面，并能运用这几种图形进行简单的镶嵌设计。

　 　⒌圆

　 　考试内容：

　 　圆，弧、弦、圆心角的关系，点与圆、直线与圆以及圆与圆的位置关系，圆周角与圆心角的关系，三角形的内心和外心，切线的性质和判定，弧长，扇形的面积，圆锥的侧面积、全面积。

　 　考试要求：

(1)理解圆及其有关概念，了解弧、弦、圆心角的关系，了解点与圆、直线与圆以及圆与圆的位置关系。

　 　(2)了解圆的性质，了解圆周角与圆心角的关系、直径所对圆周角的特征。

　 　(3)了解三角形的内心和外心。

　 　(4)了解切线的概念、切线与过切点的半径之间的关系；能判定一条直线是否为圆的切线，会过圆上一点画圆的切线。

　 　(5)会计算弧长及扇形的面积，会计算圆锥的侧面积和全面积。

　 　⒍尺规作图

　 　考试内容：

　 　基本作图，利用基本作图作三角形，过一点、两点和不在同一直线上的三点作圆。

　 　考试要求：

　 (1)能完成以下基本作图：作一条线段等于已知线段；作一个角等于已知角；作角的平分线；作线段的垂直平分线。

　 (2)能利用基本作图作三角形：已知三边作三角形；已知两边及其夹角作三角形；已知两角及其夹边作三角形；已知底边及底边上的高作等腰三角形。

　 (3)能过一点、两点和不在同一直线上的三点作圆。

　 (4)了解尺规作图的步骤，对于尺规作图题，会写已知、求作和作法(不要求证明)。

　 　⒎视图与投影

　 　考试内容：

　 　简单几何体的三视图，直棱柱、圆锥的侧面展开图，视点、视角，盲区，投影。

　 　考试要求：

　 (1)会画简单几何体(直棱柱、圆柱、圆锥、球)的三视图(主视图、左视图、俯视图)的示意图，会判断简单物体的三视图，能根据三视图描述基本几何体或实物原型。

　 (2)了解直棱柱、圆锥的侧面展开图，能根据展开图判断和制作立体模型。

　 (3)了解基本几何体与其三视图、展开图(球除外)之间的关系；知道这种关系在现实生活中的应用(如物体的包装)。

　 (4)了解并欣赏一些有趣的图形(如雪花曲线、莫比乌斯带)。

　 (5)知道物体阴影的形成，并能根据光线的方向辨认实物的阴影(如在阳光或灯光下，观察手的阴影或人的身影)。

　 (6)了解视点、视角及盲区的含义，能在简单的平面图和立体图中表示。

　 (7)了解中心投影和平行投影。

(三)函数

　 　⒈函数

　 　考试内容：

　 　平面直角坐标系，常量，变量，函数及其表示法。

　 　考试要求：

　 　(1)会从具体问题中寻找数量关系和变化规律。

　 　(2)了解常量、变量、函数的意义，了解函数的三种表示方法，会用描点法画出函数的图象，能举出函数的实际例子。

　 　(3)能结合图象对简单实际问题中的函数关系进行分析。

　 　(4)能确定简单的整式、分式和简单实际问题中的函数的自变量取值范围，并会求出函数值。

　 　(5)能用适当的函数表示法刻画某些实际问题中变量之间的关系。

　 　(6)结合对函数关系的分析，尝试对变量的变化规律进行初步预测。

　 　⒉一次函数

　 　考试内容：

　 　一次函数，一次函数的图象和性质，二元一次方程组的近似解。

　 　考试要求：

　 　(1)理解正比例函数、一次函数的意义，会根据已知条件确定一次函数表达式。

　 　(2)会画一次函数的图象，根据一次函数的图象和解析式，理解其性质(k＞0或k＜0时图象的变化情况)。

　 　(3)能根据一次函数的图象求二元一次方程组的近似解。

　 　(4)能用一次函数解决实际问题。

　 　⒊反比例函数

　 　考试内容：

　 　反比例函数及其图象。

　 　考试要求：

　 　(1)理解反比例函数的意义，能根据已知条件确定反比例函数的表达式。

　 　(2)能画出反比例函数的图象，根据图象和解析式理解其性质k＞0或k＜0时图象的变化情况)。

　 　(3)能用反比例函数解决某些实际问题。

　 　⒋二次函数

　 　考试内容：

　 　二次函数及其图象，一元二次方程的近似解。

　 　考试要求：

　 　(1)理解二次函数和抛物线的有关概念，能对实际问题情境的分析确定二次函数的表达式。

　 　(2)会用描点法画出二次函数的图象，能结合图象认识二次函数的性质。

　 　(3)会根据公式确定图象的顶点、开口方向和对称轴(公式不要求推导和记忆)，并能解决简单的实际问题。

　 　(4)会利用二次函数的图象求一元二次方程的近似解。

空 间 与 图 形

(二)方程与不等式

　 　⒈方程与方程组

　 　考试内容：

　 　方程和方程的解，一元一次方程及其解法，二元一次方程组及其解法，可化为一元一次方程的分式方程(方程中的分式不超过两个)。

　 　考试要求：

　 　(1)能够根据具体问题中的数量关系列出方程，体会方程是刻画现实世界的一个有效的数学模型。

　 　(2)会用观察、画图或计算器等手段估计方程解。

　 　(3)会解一元一次方程、简单的二元一次方程组、可化为一元一次方程的分式方程(方程中的分式不超过两个)。

　 　(4)理解配方法，会用因式分解法、公式法、配方法解简单的数字系数的一元二次方程。

　 　(5)能根据具体问题的实际意义，检验方程的解的合理性。

　 　⒉不等式与不等式组

　 　考试内容：

　 　不等式，不等式的基本性质，不等式的解集，一元一次不等式及其解法，一元一次不等式组及其解法。

　 　考试要求：

　 　(1)能够根据具体问题中的大小关系了解不等式的意义，掌握不等式的基本性质。

　 　(2)会解简单的一元一次不等式，并能在数轴上表示出解集。会解由两个一元一次不等式组成的不等式组，并会用数轴确定解集。

　 　(3)能够根据具体问题中的数量关系，列出一元一次不等式和一元一次不等式组，解决简单的问题。

(一)数与式

⒈有理数

　 　考试内容：

　 　有理数，数轴，相反数，数的绝对值，有理数的加、减、乘、除、乘方，加法运算律，乘法运算律，简单的混合运算。

　 　考试要求：

　 　(1)理解有理数的意义，能用数轴上的点表示有理数，会比较有理数的大小。

　 　(2)理解相反数和绝对值的意义，会求有理数的相反数与绝对值(绝对值符号内不含字母)。

　 　(3)理解乘方的意义，掌握有理数的加、减、乘、除、乘方的运算法则、运算律、运算顺序以及简单的有理数的混合运算(以三步为主)。

　 　(4)能用有理数的运算律简化有关运算，能用有理数的运算解决简单的问题。

　 　⒉实数

　 　考试内容：

　 　无理数，实数，平方根，算术平方根，立方根，近似数和有效数字，

　 　二次根式，二次根式的加、减、乘、除运算法则，简单的实数四则运算。

　 　考试要求：

　 　(1)了解平方根、算术平方根、立方根的概念，会用根号表示数的平方根、立方根。

　 　(2)了解开方与乘方互为逆运算，会用平方运算求某些非负数的平方根，会用立方运算求某些数的立方根，会用科学计算器求平方根和立方根。

　 　(3)了解无理数和实数的概念，知道实数与数轴上的点一一对应。

　 　(4)能用有理数估计一个无理数的大致范围。

　 　(5)了解近似数与有效数字的概念，会按要求求一个数的近似数，在解决实际问题中，能用计算器进行近似计算，并按问题的要求对结果取近似值。

　 　(6)了解二次根式的概念及其加、减、乘、除运算法则，会用运算法则进行有关实数的简单四则运算(不要求分母有理化)。

　 　⒊代数式

　 　考试内容：

　 　代数式，代数式的值，合并同类项，去括号。

　 　考试要求：

　　(1)理解用字母表示数的意义。

　　(2)能分析简单问题的数量关系，并用代数式表示。

　　(3)能解析一些简单代数式的实际背景或几何意义。

　 　(4)会求代数式的值；能根据特定的问题查阅资料，找到所需要的公式，并会代入具体的值进行计算。

　 　(5)掌握合并同类项的方法和去括号的法则，能进行同类项的合并。

　 　⒋整式与分式

　 　考试内容：

　 　整式，整式的加减法，整式乘除，整数指数幂，科学记数法。

　 　乘法公式：。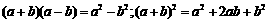

　 　因式分解，提公因式法，公式法。

　 　分式、分式的基本性质，约分，通分，分式的加、减、乘、除运算。

　 　考试要求：

　　(1)了解整数指数幂的意义和基本性质，会用科学记数法表示数(包括在计算器上表示)。

　　(2)了解整式的概念，会进行简单的整式加、减运算；会进行简单的整式乘法运算(其中的多项式相乘仅指一次式相乘)。

　 　(3)会推导乘法公式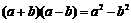：；，了解公式的几何背景，并能进行简单计算。

　 　(4)会用提公因式法和公式法(直接用公式不超过两次)进行因式分解(指数是正整数)。

　 　(5)了解分式的概念，掌握分式的基本性质，会利用分式的基本性质进行约分和通分，会进行简单的分式加、减、乘、除运算。

⒈初中毕业生数学学业考试的主要考查方面包括：基础知识与基本技能；数学活动过程；数学思考；解决问题能力；对数学的基本认识等。

⑴基础知识与基本技能考查的主要内容：

了解数产生的意义，理解代数运算的意义、算理，能够合理的进行基本运算与估算；能够在实际情境中有效的应用代数运算、代数模型及相关概念解决问题；能够借助不同的方法探索几何对象的有关性质；能够使用不同的方式表达几何对象的大小、位置与特征；能够在头脑里构建几何对象，进行几何图形的分解与组合，能对某些图形进行简单的变换；能够借助数学证明的方法确认数学命题的正确性；正确理解数据的含义，能够结合实际需要有效地表达数据特征，会根据数据结果作合理的预测；了解概率的涵义，能够借助概率模型、或通过设计活动解释一些事件发生的概率。

　　 ⑵“数学活动过程”考查的主要方面：

　 数学活动过程中所表现出来的思维方式、思维水平，对活动对象、相关知识与方法的理解深度；从事探究与交流的意识、能力和信心等。

⑶“数学思考”方面的考查应当关注的主要内容：

学生在数感与符号感、空间观念、统计意识、推理能力、应用数学的意识等方面的发展情况，其内容主要包括：

　　 能用数来表达和交流信息；能够使用符号表达数量关系，并借助符号转换获得对事物的理解；能够观察到现实生活中的基本几何现象；能够运用图形形象来表达问题、借助直观进行思考与推理；能意识到作一个合理的决策需要借助统计活动去收集信息；面对数据时能对它的来源、处理方法和由此而得到的推测性结论作合理的质疑；面对现实问题时，能主动尝试从数学角度、用数学思维方法去寻求解决问题的策略；能通过观察、实验、归纳、类比等活动获得数学猜想，并寻求证明猜想的合理性；能合乎逻辑地与他人交流等等。

　　 ⑷“解决问题能力”考查的主要方面：

　　 能从数学角度提出问题、理解问题、并综合运用数学知识解决问题；具有一定的解决问题的基本策略。

　　 ⑸“对数学的基本认识”考查的主要方面：

对数学内部统一性的认识(不同数学知识之间的联系、不同数学方法之间的相似性等)；对数学与现实、或其他学科知识之间联系的认识等等。

　 ⒉依据数学课程标准，考试要求的知识技能目标分为四个不同层次：了解(认识)；理解；掌握；灵活运用。具体涵义如下：

了解(认识)：能从具体事例中，知道或能举例说明对象的有关特征(或意义)；能根据对象的特征，从具体情境中辨认出这一对象。

理解：能描述对象的特征和由来；能明确阐述此对象与有关对象之间的区别和联系。

　　 掌握：能在理解的基础上，把对象运用到新的情境中。

　　 灵活运用：能综合运用知识，灵活、合理地选择与运用有关的方法完成特定的数学任务。

　 数学活动水平的过程性目标分为三个不同层次：经历(感受)；体验(体会)；探索。具体涵义如下：

　　 经历(感受)：在特定的数学活动中，获得一些初步的经验。

　　 体验(体会)：参与特定的数学活动，在具体情境中初步认识对象的特征，获得一些经验。

　　 探索：主动参与特定的数学活动，通过观察、实验、推理等活动发现对象的某些特征或与其它对象的区别和联系。

以下对《数学课程标准》中，数与代数、空间与图形、统计与概率、课题学习四个领域的具体考试内容与要求分述如下：

数 与 代 数

　　 教育部颁发的全日制义务教育数学课程标准(7-9年级)中：数与代数、空间与图形、统计与概率、课题学习四个部分的内容。

　　 全日制义务教育九年级学生初中数学学业考试。

教育部制订的《全日制义务教育数学课程标准(实验稿)》(以下简称《数学课程标准》)。