
题目列表(包括答案和解析)
20.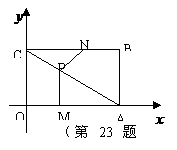 如图,平面直角坐标系中,四边形
如图,平面直角坐标系中,四边形 为矩形,点
为矩形,点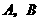 的坐标分别为
的坐标分别为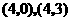 ,动点
,动点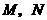 分别从
分别从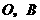 同时出发,以每秒1个单位的速度运动.其中,点
同时出发,以每秒1个单位的速度运动.其中,点 沿
沿 向终点
向终点 运动,点
运动,点 沿
沿 向终点
向终点 运动,过点
运动,过点 作
作 ,交
,交 于
于 ,连结
,连结 ,已知动点运动了
,已知动点运动了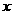 秒.
秒.
(1) 点的坐标为( , )(用含
点的坐标为( , )(用含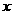 的代数式表示);
的代数式表示);
(2)试求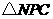 面积
面积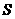 的表达式,并求出面积
的表达式,并求出面积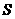 的最大值及相应的
的最大值及相应的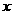 值;
值;
(3)当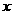 为何值时,
为何值时,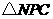 是一个等腰三角形?简要说明理由.
是一个等腰三角形?简要说明理由.
解:(1)由题意可知, ,
, ,
,
 点坐标为
点坐标为 .
.
(2)设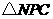 的面积为
的面积为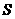 ,在
,在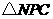 中,
中, ,
, 边上的高为
边上的高为 ,其中
,其中 .
.
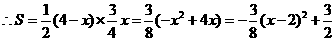 .
.
 的最大值为
的最大值为 ,此时
,此时 .
.
(3)延长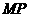 交
交 于
于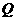 ,则有
,则有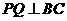 .
.
 ①若
①若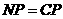 ,
,
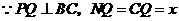 .
.
 ,
,
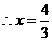 .
.
②若 ,则
,则 ,
,
 .
.
③若 ,则
,则 .
.
 ,
,
 在
在 中,
中,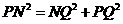 .
.
 ,
, .
.
综上所述,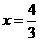 ,或
,或 ,或
,或 .
.
19.如图,在 中,
中,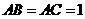 ,点
,点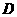 ,
, 在直线
在直线 上运动,设
上运动,设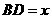 ,
, .
.
(1)如果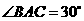 ,
,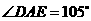 ,试确定
,试确定 与
与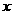 之间的函数关系式;
之间的函数关系式;
 (2)如果
(2)如果 的度数为
的度数为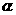 ,
, 的度数为
的度数为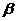 ,当
,当 满足怎样的关系式时,(1)中
满足怎样的关系式时,(1)中 与
与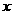 之间的函数关系式还成立,试说明理由.
之间的函数关系式还成立,试说明理由.
解:(1)在 中,
中,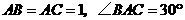 ,
,
 ,
,
 .
.
又 ,
,
 .
.
又 ,
,
 .
.
 .
.
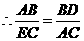 .
.
即 ,所以
,所以 .
.
(2)当 满足关系式
满足关系式 时,函数关系式
时,函数关系式 仍然成立.
仍然成立.
此时, .
.
又 ,
,
 .
.
又 仍然成立.
仍然成立.
从而(1)中函数关系式 成立.
成立.
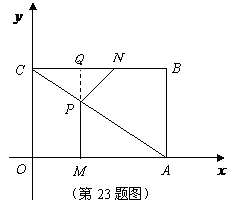
18.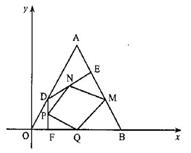 如图,边长为1的等边三角形OAB的顶点O为坐标原点,点B在x轴的正半轴上,点A在第一象限,动点D在线段OA上移动(不与O,A重合),过点D作DE⊥AB,垂足为E,过点D作DF⊥OB,垂足为F。点M,N,P,Q分别是线段BE,ED,DF,FB的中点。连接MN,NP,PQ,QM。记OD的长为t .
如图,边长为1的等边三角形OAB的顶点O为坐标原点,点B在x轴的正半轴上,点A在第一象限,动点D在线段OA上移动(不与O,A重合),过点D作DE⊥AB,垂足为E,过点D作DF⊥OB,垂足为F。点M,N,P,Q分别是线段BE,ED,DF,FB的中点。连接MN,NP,PQ,QM。记OD的长为t .
(1) 当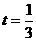 时,分别求出点D和点E的坐标;
时,分别求出点D和点E的坐标;
(2) 当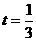 时,求直线DE的函数表达式;
时,求直线DE的函数表达式;
(3)如果记四边形MNPQ的面积为S,那么请写出面积S与变量t之间的函数关系式,并写出自变量t的取值范围,是否存在s的最大值?若存在,求出这个最大值及此时t的值;若不存在,请说明理由。

17.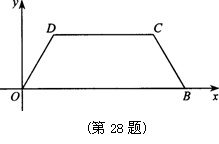 如图,在平面直角坐标系中,O为坐标原点,B(5,0),M为等腰梯形OBCD底边OB上一点,OD=BC=2,∠DMC=∠DOB=60°.
如图,在平面直角坐标系中,O为坐标原点,B(5,0),M为等腰梯形OBCD底边OB上一点,OD=BC=2,∠DMC=∠DOB=60°.
(1)求直线CB的解析式:
(2)求点M的坐标;
(3)∠DMC绕点M顺时针旋转α(30°<α<60°)后,得到∠D1MC1(点D1,C1依次与点D,C对应),射线MD1交直线DC于点E,射线MC1交直线CB于点F,设DE=m,BF=n.
求m与n的函数关系式.
解:(1)过点C作CA⊥OB,垂足为A.在Rt△ABC中,∠CAB=90°,∠CBO=60°,
0D=BC=2,∴CA=BC·sin∠CBO= , BA=BC·cos∠CBO=1.
, BA=BC·cos∠CBO=1.
 ∴点C的坐标为(4,
∴点C的坐标为(4, ).
).
设直线CB的解析式为y=kx+b,由B(5,0),C(4, ),
),
得 解得
解得
∴直线CB的解析式为y=- x+5
x+5 .
.
(2)∵∠CBM+∠2+∠3=180°,∠DMC+∠1+∠2=180°,∠CBM=∠DMC=∠DOB=60°
∴∠2+∠3=∠1+∠2,∴∠1=∠3.
 ∴△ODM∽△BMC.
∴△ODM∽△BMC.

∴OD·BC=BM·OM.
∵B点为(5,0),∴OB=5.
设OM=x,则BM=5-x.
∵OD=BC=2,∴2×2=x(5-x).
 解得x1=1,x2=4.
解得x1=1,x2=4.
∴M点坐标为(1,0)或(4,0).
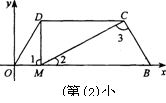
(3)(I)当M点坐标为(1,0)时,
如图①,OM=1,BM=4.
∵DC∥OB,∴∠MDE=∠DMO.
又∠DMO=∠MCB,∴∠MDE=∠MCB.
∵∠DME=∠CMF=a,∴△DME∽△CMF.


∴CF=2DE.
∵CF=2+n,DE=m,
∴2+n=2m,即m=1+ (0<n<4).
(0<n<4).
(Ⅱ)当M点坐标为(4,0)时,如图②.
OM=4,BM=1.
同理可得△DME∽△CMF,

∴DE=2CF.
∵CF=2-n,DE=m,∴m=2(2-n),即m=4-2n( <n<1).
<n<1).
16.已知抛物线y=ax2+bx+c经过A,B,C三点,当x≥0时,其图象如图所示.
(1)求抛物线的解析式,写出抛物线的顶点坐标;
(2)画出抛物线y=ax2+bx+c当x<0时的图象;
(3)利用抛物线y=ax2+bx+c,写出x为何值时,y>0.

解:(1)由图象,可知A(0,2),B(4,0),C(5,-3),
得方程组 解得
解得
∴抛物线的解析式为
顶点坐标为
(2)所画图如图.
(3)由图象可知,当-1<x<4时,y>0.
15.直线 分别与
分别与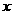 轴、
轴、 轴交于B、A两点.
轴交于B、A两点.
⑴求B、A两点的坐标;
 ⑵把△AOB以直线AB为轴翻折,点O落在平
⑵把△AOB以直线AB为轴翻折,点O落在平
面上的点C处,以BC为一边作等边△BCD
求D点的坐标.
解:如图(1)令x=0,由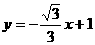 得 y=1
得 y=1
令y=0,由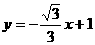 得
得
∴B点的坐标为( ,0),A点的坐标为(0,1)
,0),A点的坐标为(0,1)
(2)由(1)知OB= ,OA=1
,OA=1
∴tan∠OBA= =
=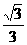 ∴∠OBA=30°
∴∠OBA=30°
∵△ABC和△ABO关于AB成轴对称
∴BC=BO= ,∠CBA=∠OBA=30° ∴ ∠CBO=60°
,∠CBA=∠OBA=30° ∴ ∠CBO=60°
过点C作CM⊥x轴于M,则在Rt△BCM中
CM=BC×sin∠CBO= ×sin60°=
×sin60°=
BM=BC×cos∠CBO= ×cos60°=
×cos60°= ∴OM=OB-BM=
∴OM=OB-BM= -
- =
=
∴C点坐标为( ,
, )
)
连结OC
∵OB=CB,∠CBO=60°
∴△BOC为等边三角形
过点C作CE∥x轴,并截取CE=BC则∠BCE=60°
 连结BE则△BCE为等边三角形.
连结BE则△BCE为等边三角形.
作EF⊥x轴于F,则EF= CM= ,BF=BM=
,BF=BM=
OF=OB+BF= +
+ =
=
∴点E坐标为( ,
, )
)
∴D点的坐标为(0,0)或( ,
, )
)
14.已知抛物线y=x²-4x+1.将此抛物线沿x轴方向向左平移4个单位长 度,得到一条新的抛物线.
度,得到一条新的抛物线.
⑴求平移后的抛物线解析式;
⑵若直线y=m与这两条抛物线有且只有四个交点,求实数m的取值范围;
⑶若将已知的抛物线解析式改为y=ax²+bx+c(a>0,b<0),并将此抛物线沿x轴方向向左平移 - 个单位长度,试探索问题⑵.
个单位长度,试探索问题⑵.
(1)解:
配方,得 ,
,
向左平移4个单位,得
∴平移后得抛物线的解析式为
(2)由(1)知,两抛物线的顶点坐标为(2,3),(-2,-3)
解 ,得
,得
∴两抛物线的交点为(0,1)
由图象知,若直线y=m与两条抛物线有且只有四个交点时,
m>-3且m≠1
(3)由 配方得,
配方得,
向左平移 个单位长度得到抛物线的解析式为
个单位长度得到抛物线的解析式为

∴两抛物线的顶点坐标分别为 ,
,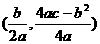
解 得,
得,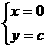
∴两抛物线的交点为(0,c)
由图象知满足(2)中条件的m的取值范围是:
m> 且m≠c
且m≠c
13.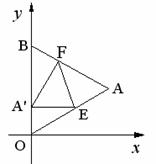 如图,△OAB是边长为
如图,△OAB是边长为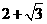 的等边三角形,其中O是坐标原点,顶点B在
的等边三角形,其中O是坐标原点,顶点B在 轴正方向上,将△OAB 折叠,使点A落在边OB上,记为A′,折痕为EF.
轴正方向上,将△OAB 折叠,使点A落在边OB上,记为A′,折痕为EF.
(1)当A′E//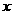 轴时,求点A′和E的坐标;
轴时,求点A′和E的坐标;
(2)当A′E//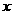 轴,且抛物线
轴,且抛物线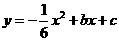 经过点A′和E时,求抛物线与
经过点A′和E时,求抛物线与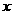 轴的交点的坐标;
轴的交点的坐标;
(3)当点A′在OB上运动,但不与点O、B重合时,能否使△A′EF成为直角三角形?若能,请求出此时点A′的坐标;若不能,请你说明理由.
解:(1)由已知可得∠A,OE=60o , A,E=AE
由A′E//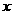 轴,得△OA,E是直角三角形,
轴,得△OA,E是直角三角形,
设A,的坐标为(0,b)
AE=A,E=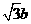 ,OE=2b
,OE=2b

所以b=1,A,、E的坐标分别是(0,1)与( ,1)
,1)
(2)因为A,、E在抛物线上,所以

所以 ,函数关系式为
,函数关系式为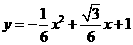
由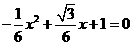 得
得
与x轴的两个交点坐标分别是(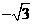 ,0)与(
,0)与(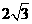 ,0)
,0)
(3)不可能使△A′EF成为直角三角形.
∵∠FA,E=∠FAE=60o,若△A′EF成为直角三角形,只能是∠A,EF=90o或∠A,FE=90o
若∠A,EF=90o,利用对称性,则∠AEF=90o, A,、E、A三点共线,O与A重合,与已知矛盾;
同理若∠A,FE=90o也不可能
所以不能使△A′EF成为直角三角形.
12.抛物线y=3(x-1) +1的顶点坐标是( A )
+1的顶点坐标是( A )
A.(1,1) B.(-1,1) C.(-1,-1) D.(1,-1)
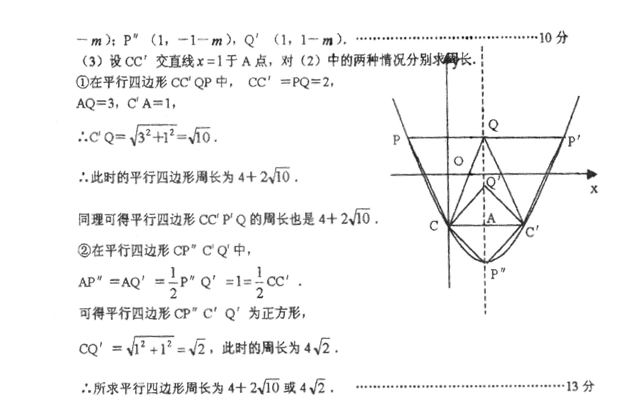
11.已知:抛物线 (m>0)与y轴交于点C,C点关于抛物线对称轴的对称点为C′点.
(m>0)与y轴交于点C,C点关于抛物线对称轴的对称点为C′点.
(1)求C点、C′点的坐标(可用含m的代数式表示)
 (2)如果点Q在抛物线的对称轴上,点P在抛物线上,以点C、C′、P、Q为顶点的四边形是平行四边形,求Q点和P点的坐标(可用含m的代数式表示)
(2)如果点Q在抛物线的对称轴上,点P在抛物线上,以点C、C′、P、Q为顶点的四边形是平行四边形,求Q点和P点的坐标(可用含m的代数式表示)
(3)在(2)的条件下,求出平行四边形的周长.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com