18．如图，E是矩形ABCD的边AD上一点，且BE＝ED，P是对角线BD上任意一点，PF⊥BE，PG⊥AD，垂足分别为F、G．求证：PF+PG＝AB．

[提示]延长GP交BC于H，只要证PH＝PF即可，所以只要证∠PBF＝∠PBH．

[答案]∵　 BE＝DE，

∴　 ∠EBD＝∠EDB．

∵　 在矩形ABCD中，AD∥BC，

∴　 ∠DBC＝∠ADB，

∴　 ∠EBD＝∠CBD．

延长GP交BC于H点．

∵　 PG⊥AD，

∴　 PH⊥BC．

∵　 PF⊥BE，P是∠EBC的平分线上．

∴　 PF＝PH．

∵　 四边形ABHG中，

∠A＝∠ABH＝∠BHG＝∠HGA＝90°．

∴　 四边形ABHG为矩形，

∴　 AB＝GH＝GP+PH＝GP+PF

故　 PF+PG＝AB．

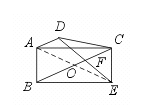
17．已知：如图，梯形ABCD中，AD∥BC，过C作CE∥AB且CE＝AB，连结

DE交BC于F．求证：DF＝EF．

[提示]连结AE交BC于O，要证DF＝EF，因为AD∥BC，所以只要证OA＝OE，只要证四边形ABEC为平行四边形．

[答案]连结AE交BC于O点，

∵　 CEAB，

∴　 四边形ABEC为平行四边形，

∴　 OA＝OE．

又　 AD∥BC，

∴　 DF＝EF．

16．如图，矩形纸片ABCD中，AB＝3 cm，BC＝4 cm．现将A，C重合，使纸片

折叠压平，设折痕为EF，试求AF的长和重叠部分△AEF的面积．

[提示]把AF取作△AEF的底，AF边上的高等于AB＝3．

由折叠过程知，EF经过矩形的对称中心，FD＝BE，AE＝CE＝AF．由此可以在

△ABE中使用勾股定理求AE，即求得AF的长．

[答案]如图，连结AC，交EF于点O，

由折叠过程可知，OA＝OC，

∴　 O点为矩形的对称中心．E、F关于O点对称，B、D也关于O点对称．

∴　 BE＝FD，EC＝AF，

由EC折叠后与EA重合，

∴　 EC＝EA．

设AF＝x，则BE＝FD＝AD－AF＝4－x，AE＝AF＝x．

在Rt△ABE中，由勾股定理，得

AB²+BE²＝AE²，即　 3²+(4－x) ²＝x²．

解得　 x＝．

∴　 S_△AEF＝×3×＝(cm²)

故AF的长为cm，△AEF的面积为cm²．

15．如图，一个等腰梯形的两条对角线互相垂直，且中位线长为l，求这个等腰梯形的高．

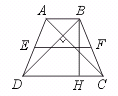
[提示]如下图，过B点作AC的平行线．

[答案]过B作BG∥AC，交DC的延长线于G点．

在梯形ABCD中，AB∥DC，

∴　 四边形ABGC为平行四边形．

∴　 CG＝AB，BG＝AC．

∵　 EF为梯形中位线，

∴　 DG＝DC+AB＝2 EF＝2 l．

∵　 AC⊥BD且AC＝BD．

∴　 BG⊥BD且BG＝BD．

∴　 △BDG为等腰直角三角形．

∴　 高BH＝DG＝l．

14．如图，将边长为1的正方形ABCD绕A点按逆时针方向旋转30°，至正方形

AB′C′D′，则旋转前后正方形重叠部分的面积是________．

[提示]设CD与B′C′的交点为M，则AM为两正方形的对称轴．又设MD＝x，则AM＝2 x，用勾股定理列方程并解之即可．

[答案]．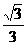

13．如图，梯形ABCD中，△ABP的面积为20平方厘米，△CDQ的面积为35平方厘米，则阴影四边形的面积等于______平方厘米．

[提示]连结MN．S_△MNP＝S_△ABP，S_△MNQ＝S_△CDQ．

[答案]55．

12．如图，如果四边形CDEF旋转后能与正方形ABCD重合，那么在图形所在平面内，可以作为旋转中心的点的个数为______．

[提示]施转中心必须在公共边CD上．

[答案]3．

11．用任意两个全等的直角三角形拼下列图形：

①平行四边形　 ②矩形　　　　　 ③菱形

④正方形　　　 ⑤等腰三角形　　 ⑥等边三角形

其中一定能够拼成的图形是_______(只填题号)．

[答案]①②⑤．

10．如图，P是□ABCD内的一点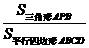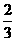，＝，则＝______．

[提示]过P点分别作AB和BC的平行线，与□ABCD的边相交，找出4对全等三角形．由此可见，△ABP与△CDP的面积之和为□ABCD面积的一半．

[答案]．

9．一个多边形的一个内角的补角与其他内角的和恰为500°，那么这个多边形的边数是______．

[提示]由于五边形内角和为540°＞500°，所以多边形的边数不可能超过5．显然它不可能是三角形．因此分四边形、五边形两种情况验证是否存在符合要求的图形．

[答案]4或5．