
题目列表(包括答案和解析)
19.
1. 6 2. D.3.( B ) 4.( C)5 ( B )6、(B 7、(D8、(D)9、(①AB∥CD;②AC⊥BD;③AO=OC; 10.( B ).11.C. 12.( C )13.B.14(C)15、 D. 16. (D ) 17.(_70°18、 ( D)
例1 (n - 2)·1800 =3600.解得 n=4. 例2 答案:B. 例3( B )
 例4_____4cm,6cm ___
例4_____4cm,6cm ___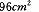 _____.
_____.
例5答案:∠B=60°.
例6.中心对称的运用
例7
例8 .(C)
例9 点A是旋转中心,顺时针方向旋转了45.
基础达标
29、(2005广东省)如图,等腰梯形ABCD中,AD∥BC,M、N分别是AD、BC的中点,E、F分别是BM、CM的中点。
 (1)求证:四边形MENF是菱形;
(1)求证:四边形MENF是菱形;
(2)若四边形MENF是正方形,请探索等腰梯形ABCD的高和底边BC的数量关系,并证明你的结论。
四边形及平移旋转对称答案
27.如图,已知正方形ABCD的边长为2.如果将线段BD 绕着点B旋转后,点D落在CB的延长线上的D′点处,
 那么
那么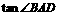 ′等于__________
′等于__________
26.(2004.上海)如图1,边长为3的正方形ABCD绕点C按顺时针方向旋转30 °后得到正方形EFCG,EF交AD于点H,那么DH的长为________.
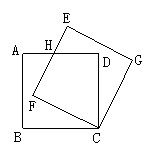
25、如图,在□  中,
中, 是对角线
是对角线 的中点,过点
的中点,过点 作
作 的垂线与边
的垂线与边 、
、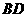 分别交于
分别交于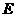 、
、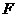 ,求证:四边形
,求证:四边形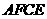 是菱形.
是菱形.

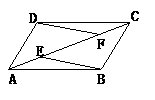
25.如图,E、F是□ABCD的对角线AC上两点,AE=CF.
求证:(1)△ABE≌△CDF.(2)BE∥DF.
(B层)
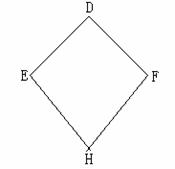
24.三月三,放风筝,小明制了一个风筝,如右图,且DE=DF,EH=FH,小明不用度量就知道∠DEH = ∠DFH。请你用所学过的数学知识证明之。(提示:可连结DH,证明 ΔDHE≌ΔDHF或连结EF,通过证明等腰三角形得证。)
23、(2005常州市)如图,在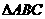 中,点
中,点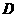 、
、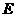 、
、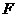 分别在
分别在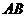 、
、 、
、 上,
上, ,
,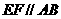 ,且
,且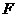 是
是 的中点.
的中点.
求证: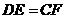
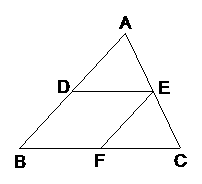
证: ⑴∵AD∥BC ∴AD∥CE 又∵DE∥AC ∴四边形ACED是平行四边形 ⑵过D点作DF⊥BE于F点 ∵DE∥AC,AC⊥BD ∴DE⊥BD,即∠BDE=90°
由⑴知DE=AC,CE=AD=3 ∵四边形ABCD是等腰梯形 ∴AC=DB
∴DE=DB ∴△DBE是等腰直角三角形,∴△DFB也是等腰直角三角形
∴DF=BF=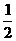 (7-3)+3=5 (也可运用:直角三角形斜边上的中线等于斜边的一半“)
(7-3)+3=5 (也可运用:直角三角形斜边上的中线等于斜边的一半“)
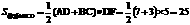 注:⑴过对角线交点O作OF⊥BC于F,延长FO交AD于H,于是OH⊥AD由△ABC≌△DCB,得到△OBC是等腰直角三角形,OF=
注:⑴过对角线交点O作OF⊥BC于F,延长FO交AD于H,于是OH⊥AD由△ABC≌△DCB,得到△OBC是等腰直角三角形,OF=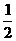 BC=
BC= 同理OH=
同理OH=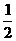 AD=
AD= ,高HF=
,高HF= ⑵过A作AF⊥BC于F,过D作DH⊥BC于H,由△AFC≌△DHB 得高AF=FC=
⑵过A作AF⊥BC于F,过D作DH⊥BC于H,由△AFC≌△DHB 得高AF=FC=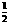 (AD+BC)=5⑶
(AD+BC)=5⑶ (进行计算)
(进行计算)
解:(1)当CE=4时,四边形ABED是等腰梯形。 理由如下:
在BC上截取CE=AD,连结DE、AE,∵AD∥BC, ∴四边形AECD是平行四边形。
∴AE=CD=BD。 ∵BE=12-4=8>4,即BE>AD, ∴AB不平行于DE,
∴四边形ABED是梯形。 ∵AE∥CD,CD=BD, ∴∠AEB=∠C=∠DBC。
在△ABE和△DEB中,
 ∴△ABE≌△DEB (SAS)。
∴AB=DE,
∴△ABE≌△DEB (SAS)。
∴AB=DE,
∴四边形ABED是等腰梯形。 (也可不作辅助线,通过证明△ABD≌EDC而得AB=DE)
(2)当C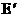 =6时,四边形AB
=6时,四边形AB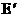 D是直角梯形。 理由如下: 在BC上取一点
D是直角梯形。 理由如下: 在BC上取一点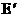 ,使C
,使C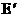 =B
=B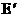 =
=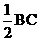 =6,连结D
=6,连结D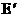 , ∵BD=CD ∴D
, ∵BD=CD ∴D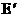 ⊥BC 又∵B
⊥BC 又∵B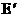 ≠AD,AD∥B
≠AD,AD∥B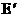 , ∴AB不平行于D
, ∴AB不平行于D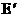 ∴四边形AB
∴四边形AB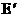 D是直角梯形。
D是直角梯形。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com