13. 下图中，图(1)是一个扇形AOB，将其作如下划分：

第一次划分：如图(2)所示，以OA的一半OA₁为半径画弧，再作∠AOB的平分线，得到扇形的总数为6个，分别为：扇形AOB，扇形AOC，扇形COB，扇形A₁OB₁，扇形A₁OC₁，扇形C₁OB₁；

第二次划分：如图(3)所示，在扇形C₁OB₁中，按上述划分方式继续划分，可以得到扇形的总数为11个；

第三次划分：如图(4)所示：…依次划分下去。

　　　　 (1)　　　　　　 (2)　　　　　　　　 (3)　　　　　　　　 (4)

(1)根据题意，完成下表：

　 (2)根据上表，请你判断按上述划分方式，能否得到扇形的总数为2005个？为什么？

12. 如图，在平面直角坐标系中，CA⊥x轴于点A(1，0)，DB⊥x轴于点B(3，0)，直线CD与x轴、y轴分别交于点F、E，S_{四边形ABDC}=4。

　 (1)若直线CD的解析式为y=kx+3，求k的值；

(2)试探索在x轴正半轴上存在几个点P，使△EPF为等腰三角形，并求出这些点的坐标。

11. 已知，Rt△AOB中，∠AOB=90°，OA=3cm，OB=4cm，以O为坐标原点建立如图所示的平面直角坐标系，设P、Q分别为AB边、OB边上的动点，它们同时分别从点A、O向B点匀速运动，移动的速度为1cm/s，设P、Q移动时间为ts(0≤t≤4)。

　 (1)过点P作PM⊥OA于M，证明，

并求出点P的坐标(用t表示)。

　 (2)求△OPQ的面积S(cm²)与移动时间t(s)之间的函数关系式；当t为何值时，S有最大值，并求出S的最大值。

　 (3)请你探索：当t为何值时，△OPQ为直角三角形。

10. 在数学活动中，小明为了求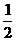++++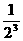…+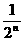的值(结果用n表示)，设计如图1所示的几何图形。

　 (1)请你利用这个几何图形求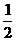++++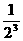…+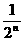的值为　　　　 。

　 (2)请你利用图2，再设计一个能求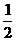++++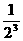…+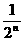的值的几何图形。

　　　　　　　　　 (1)　　　　　　　　　　　　　　 (2)

9. 在平面直角坐标系中，横坐标、纵坐标都为整数的点称为整点，观察图中每一个正方形(实线)四条边上的整点的个数，请你猜测由里向外第10个正方形(实线)四条边上的整点个数共有　　　　 个。

8. 用同样大小的黑、白两种颜色的棋子摆设如下图所示的正方形图案，则第n个图案需要用白色棋子　　　　　　 枚(用含有n的代数式表示)。

○ ○ ○　　　 ○ ○ ○ ○　　　 ○ ○ ○ ○ ○

　　　　　　　 ○ ● ● ○　　　 ○ ● ● ● ○

○ ● ○　　　 ○ ● ● ○　　　 ○ ● ● ● ○

　　　　　　　 ○ ○ ○ ○　　　 ○ ● ● ● ○

○ ○ ○　　　 　　　　　　　　　○ ○ ○ ○ ○

7. 如图，摆第1个“小屋子”要5枚棋子，摆第二个要11枚棋子，摆第3个要17枚棋子，则摆第30个“小屋子”要　　　 枚棋子。

　　　　　　　　 (1)　 　　　(2)　　　　　 (3)

6. 已知n(n≥2)个点P₁、P₂、P₃…P_n在同一平面内，且其中没有任何三点在同一直线上，设Sn表示过这n个点中的任意2个点所作的所有直线的条数，显然S₂=1，S₃=3，S₄=6，S₅=10…，由此推断S_n=　　　　　　　 。

5. 将正奇数如下表排列：　　　　　　　　　　　　　　　　　　　　　

按表中的排列规则，数　　　　　　　　　　　　　　　　　　　　　　

2005应排在第　 行第　 列。 　　　　　　　　　　　　　　　　　　　

4. 观察下面一列数：　　　　 1

　　　　　　　　　　 -2　　 3　 -4

　　　　　　　　　　 5　 -6　　 7　　 -8　　 9

　　　　　　　 -10　 11　 -12　 13　 -14　 15　 -16

　　　　　　 　　　……　 ……

按上述规律排下去，那么第10行从左边数第9个数是　　　　 。

列 行	一	二	三	四	五
一		1	3	5	7
二	15	13	11	9
三		17	19	21	23
四	…	…	27	25