
题目列表(包括答案和解析)
30、 (参考题) 在一次实践活动中,某课题学习小组用测倾器、皮尺测量旗杆的高度,他们设计了如下方案(如图19-16)
      M MC α E A N 图19-16 |
① 在测点A安置测倾器,测得旗杆顶部M的仰角∠MCE=α;
② 量出测点A到旗杆底部N的水平距离AN=m;
③ 量出测倾器的高度AC=h
根据上述测量数据,即可求出旗杆的高度MN。
如果测量工具不变,请仿照上述过程,设计一个测量某小山高度(如图19-17)的方案;
     M MN 图19-17 |
⑴ 在图19-17中,画出你测量小山高度MN的示意图(标上适当字母)
⑵写出你的设计方案。



29、 (8分)如图19-15所示,A、B为两个村庄,AB、BC、CD为公路,BD为田地,AD为河宽,且CD与AD互相垂直,现在要从E点开始铺设通往村庄A、村庄B的一条电缆,共有如下两种铺设方案:
方案一:E→D→A→B
方案二:E→C→B→A。
经测量得,AB=4 千米,BC=10千米,CE=6千米,
千米,BC=10千米,CE=6千米,
      C
C E
EB A D 图19-15 |
∠BDC=450, ∠ABD=150,已知地下电缆的修建费为2万元/千米,水下电缆的修建费为4万元/千米。
① 求出河宽AD(结果保留根号);
② 求公路CD的长;
③ 哪种方案铺设电缆的费用低?请说明你的理由。
28、
(8分) 如图19-14,不透明圆锥体DCE放在直线BP所在的水平面上,且BP过底面圆心,其高为2 m,底面半径为2m。某光源位于点A处,照射圆锥体在水平面上留下的影长BE=4m。
m,底面半径为2m。某光源位于点A处,照射圆锥体在水平面上留下的影长BE=4m。
① 求∠B的度数;
② 若∠ACP=2∠B,求光源A距平面的高度。
A  D
D  B E C P 图19-14 |
27、
(8分) 如图19-13,是一座人行天桥的示意图,天桥高10m,坡面的倾斜角为450,为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面的倾斜角为300。若新坡脚前需留3m的人行道,问离原坡脚10m的建筑物是否需要拆除?请说明理由。( ≈1.414,
≈1.414, ≈1.732)
≈1.732)
0.8米
450 A 1.2米 B
图19-12

C 10米   D D 3 A B 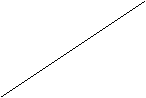  图19-13 图19-13 |
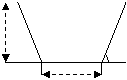
26、 (8分) 某村计划开挖一条长为1500m的水渠,渠道的断面为等腰梯形,渠道深0.8m,下底宽1.2m,坡度为450,(如图19-12),实际开挖渠道时,每天比原计划多挖土20m3,结果比原计划提前4天完工,求原计划每天挖土多少立方米?
 D
C
D
C
25、
(7分)某片绿地的形状如图19-11,∠A=600。AB⊥BC, AD⊥CD,AB=200m,CD=100m,求AD、BC的长(精确到1m, ≈1.732)
≈1.732)
      A A D B C 图19-11 |
24、 (7分)如图19-10。A、B、C三个村庄在一条东西走向的公路上,AB=2千米,在B村的正北方向有一个D村,测得∠DAB=450,∠DCB=280,今将△ACD区域进行规划,除其中面积为0.5平方千米的水塘外,准备把剩余区域的一半作绿化用地,试求绿化用地的面积(结果精确到0.1平方千米,sin280=0.4695,cos280=0.8829,tan280=0.5317,cot280=1.8808)
23、 已知在Rt△ABC中,∠C=900,则关于x的一元二次方程x2cotA-2x+cotB=0的根的情况是( )
  D D
A B C 图19-10 |
A. 有两个不相等的实数根 B. 有两个相等的实数根 C. 没有实数根 D. 根的情况由∠A、∠B的值确定。
22、 已知,如图19-9,梯形ABCD中,AD∥BC,∠B=450,∠C=1200,AB=8,则CD的长为( )
A.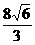 B.4
B.4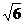 C.
C.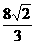 D.4
D.4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com