8．若两个角互补，则其中一定有一个角是钝角……………………………………(　　 )

[提示]

“互补”即两角和为180°．想一想：这里的两个角可能是怎样的两个角？

[答案]

×．

[点评]

两角互补，这里的两角有两种情形，如图：

图(1)　　　　　 图(2)

因此，互补的两个角中，可能有一个是钝角，也可能两个角都是直角，因此在作出判断前必须全面地考虑，这就要求有“分类讨论”的思想，“分类讨论”是数学中重要的思想方法之一．

7．互余且相等的两个角都是45°的角…………………………………………(　　 )

[提示]

“互余”即两角和为90°．

[答案]

√．

[点评]

设相等的两个角为x°，由“互余”得，2x＝90，∴ x＝45(度)，以正确的计算为依据，也是作判断题的方法之一．注意，角度是一个带单位的数．设未知数时，未知量带单位，则列式中即可不用带单位．这与解其他类型的应用题格式相同．

6．角的边的长短，决定了角的大小．

[提示]

角的大小，与组成角的两条射线张开的程度相关，或者说与射线绕着它的端点旋转过的平面部分的大小相关，与角的边画出部分的长短无关．

[答案]

×．

[点评]

我们在现实生活中看到的直线或射线，其实大多数以线段的形式出现的，所以在运用直线或射线概念时，千万别忘了它们的几何意义，否则就要出错．

5．两条射线组成的图形叫做角……………………………………………………(　　 )

[提示]

有公共端点的两条射线组成的图形叫做角．

[答案]

×．

[点评]

“角”的构成有两个条件：①有公共端点；②两条射线组成的图形．两者缺一不可，按题中的叙述，可以画出这样的图形(如下图)，显然这个图形不是角．

4．两条直相交，只有一个交点……………………………………………………(　 　)

[提示]

两条不同的直线，如果它们有一个公共点，我们就说它们相交，若两条直线相交，有两个公共点，那么根据直线公理：经过两点有且只有一条直线，则这两条直线实际上是同一条直线了．同样两条不同的直线不能有三个或更多的公共点．

[答案]

√．

3．连结两点的线段，叫做这两点间的距离…………………………………………(　　 )

[提示]

连结两点的线段的长度，叫做这两点的距离．

[答案]

×．

[点评]

“线段”表示的是“图形”，而“距离”指的是线段的“长度”，指的是一个“数”，两者不能等同．

2．射线AP和射线PA是同一条射线………………………………………………(　　 )

[提示]

表示射线端点的字母要写在前，另一个字母写在后，端点不同的射线不是同一条射线．

[答案]

×．

1．经过三点中的每两个，共可以画三条直线…………………………………(　　 )

[提示]

平面内三点可以在同一条直线上，也可以不在同一条直线上．

[答案]

×．

[点评]

要注意，三个点的相互位置共有两种情况，如图

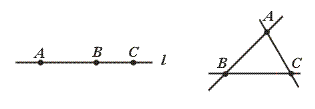
(1)　　　　　(2)

因此，平面内经过三点中每两个的直线可以是同一条，也可以是三条，必须把上面两种情况全部考虑到，再分类解决，若只考虑其中的第二种情况，判断就会出错．

(六)解答题(每小题5分，共30分)

29．如图，线段AB被点C、D分成了3︰4︰5三部分，且AC的中点M和DB的中点N之间的距离是40 cm，求AB的长．

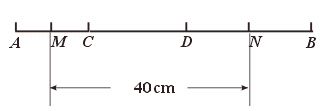
[提示]引入未知数，列方程求解．

[答案]60 cm．

设一份为x cm，则AC＝3 x cm，CD＝4 x cm，DB＝5 x cm．

∵　 M是AC的中点，

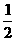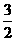∴　 CM＝AC＝x cm．

∵　 N是DB的中点，

∴　 DN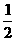＝DB＝x cm．

∵　 MN＝MC+CD+DN，

又　 MN＝40 cm，

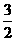∴ 　x+4 x+x＝40，

　　　　　　　　　　　　8x＝40．

∴ 　　　 x＝5．

∴ 　AB＝AC+CD+DB＝12 x＝12×5＝60(cm)．

30．一个角的补角与20°角的和的一半等于这个角的余角的3倍，求这个角．

[提示]两角互余和为90°，两角互补和为180°．设这个角为x°，列方程求解．

[答案]68°．

设这个角为x°，根据题意得

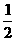(180°－x+20°)＝3(90°－x)，

100°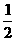－x＝270°－3 x，

x＝170°，

∴ 　　　　　 　x＝68°，

即这个角为68°．

31．如图，直线AB、CD相交于点O，OB平分∠EOD，∠COE＝100°，求∠AOD和∠AOC的度数．

[提示]由∠COE＝100°，OB平分∠EOD，可求出∠BOD的度数，进而求出∠AOD和∠AOC的度数．

[答案]∠AOD＝140°，∠AOC＝40°．

计算过程如下：

∵ 　∠COD＝180°，∠COE＝100°(已知)，

∴ 　∠EOD＝∠COD－∠COE＝180°－100°＝80°．

∵ 　OB平分∠EOD(已知)，

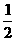∴ 　∠BOD＝∠EOD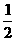＝×80°＝40°(角平分线定义)．

∵ 　∠AOB＝180°(平角定义)，

∴ 　∠AOD＝∠AOB－∠BOD＝180°－40°＝140°，

∠AOC＝∠COD－AOD＝180°－140°＝40°．

[点评]由计算可知，∠BOC＝∠COE+∠EOB＝100°+40°＝140°．

∴ 　∠AOD＝∠BOC，又知∠AOC＝∠BOD，这是一种偶然的巧合，还是必然的结果？在第二章“相交线、平行线”中可揭开这个谜．

32．如图，∠AOC、∠BOD都是直角，且∠AOB与∠AOD的度数比是2︰11，求∠AOB和∠BOC的度数．

[提示]设∠AOB＝x°，∠BOC＝y°，列方程组求解．

[答案]∠AOB＝20°，∠BOC＝70°．

计算过程如下：

∵ 　∠AOC、∠BOD都是直角(已知)，

∴ 　∠AOB+∠BOC＝90°，∠COD+∠BOC＝90°(直角的定义)．

∴ 　∠AOB＝∠COD(同角的余角相等)．

设∠AOB＝∠COD＝x° ，∠BOC＝y°．

由题意得

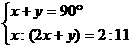
即　　

解得

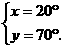
即∠AOB＝20°，∠BOC＝70°．

33．考察队从营地P处出发，沿北偏东60°前进了5千米到达A地，再沿东南方向前进到达C地，C地恰好在P地的正东方向．

(1)按1︰100 000画出考察队行进路线图．

(2)量出∠PAC、∠ACP的度数(精确到1°)．

(3)测算出考察队从A到C走了多少千米？此时他们离开营地多远？(精确到0.1千米)．

[提示]比例尺＝图上距离︰实际距离，先根据1︰100 000的比例尺算出PA的图上距离，然后再画图．

[答案](1)考察队行进的路线图如右图所示．

(2)量得∠PAC＝105°，∠ACP＝45°．

(3)算得AC≈3.5千米；PC≈6.8千米．

略解如下：

(1)算出PA的图上距离，由5千米＝500 000厘米．

∴ 　＝．

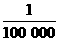∴ 　PA＝5厘米．

(3)量得AC≈3.5厘米，PC＝6.8厘米．

∴ 　AC的实际距离约为：3.5厘米×100 000＝350 000厘米＝3.5千米；

PC的实际距离约为：6.8厘米×100 000＝680 000厘米＝6.8千米．

34．已知直角∠AOB，以O为顶点，在∠AOB的内部画出100条射线，则以OA、OB及这些射线为边的锐角共有多少个？若以O为项点，在∠AOB的内部画出几条射线(n≥1的自然数)，则OA、OB以及这些射线为边的锐角共有多少个？

[提示]在∠AOB的内部，以O为顶点，画1，2，3，4条射线，数数各有多少个锐角，找出规律，再计算100条射线、n条射线所构成的锐角的个数．

[答案]5 150个锐角；个锐角．

1条射线　 1+1＝2(个锐角)，

2条射线　 2+2+1＝5(个锐角)，

3条射线　 3+3+2+1＝9(个锐角)，

4条射线　 4+4+3+2+1＝14(个锐角)，

……

100条射线 　100+100+99+98+…+3+2+1

＝100+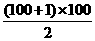

＝100+5 050

＝5 150(个锐角)，

n条射线 　 n+n+(n－1)+(n－2)+…+3+2+1

＝n+

＝(个锐角)．

[点评]数锐角的个数与数线段的条数一样，以OA为始边，另一条射线为角的终边依次去数，这样可不遗漏不重复地将要数的锐角个数数准确．注意∠AOB是直角，故这个角不在计数的范围内．

若题目改成：已知∠AOB，以O为顶点，在∠AOB的内部画出n条射线，n为非零自然数，以OA、OB以及这些射线为边的角共有多少个？

答案是：共有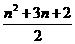个角．

(五)画图题(第26小题4分，第27小题5分，第28小题6分，共15分)

26．已知：线段a、b、c(b＞c)，画线段AB，使AB＝2a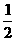－(b－c)．

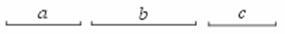
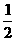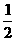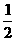[提示]AB＝2a－(b－c)＝2a+c－b．

[答案]方法一：

量得　 a＝20 mm，b＝28 mm，c＝18 mm．

AB＝2a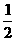－(b－c)

＝2×20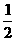－(28－18)

＝40－5

＝35(mm)．

画线段AB＝35 mm(下图)，

则线段AB就是所要画的线段．

方法二：

画法如下(如上图)：

(1)画射线AM．

(2)在射线AM上依次截取AC＝CD＝a，DE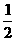＝c．

(3)在线段EA上截取E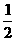B＝b．

则线段AB就是所要画的线段．

27．已知∠a ，∠b ，∠g ，画∠AOB，使∠AOB＝2∠a+∠b－∠g ．

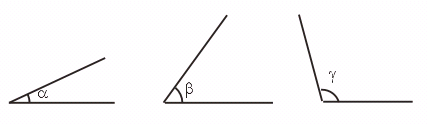
[提示]方法一：先量、后算、再画；

方法二：叠加法，逐步画出．

[答案]方法一：

量得∠a ＝25°，∠b ＝54°，∠g ＝105°，

∠AOB＝2∠a +∠b －∠g

＝2×25°+54°－×105°

＝50°+54°－35°

＝69°．

画∠AOB＝69°，则∠AOB就是所要画的角．

方法二：

画法：

(1)画∠AOC＝∠a ，

(2)以O为顶点，OC为一边在∠AOC的外部画∠COD＝∠a ．

(3)以O为顶点，OD为一边在∠AOD的外部画∠DOE＝∠b ．

(4)以O为顶点，OE为一边在∠EOA的内部画∠EOB＝∠g ．

则∠AOB就是所要画的角．

28．读句画图，填空：

(1)画线段AB＝40 mm；

(2)以A为顶点，AB为一边，画∠BAM＝60°；

(3)以B为顶点，BA为一边，在∠BAM的同侧画∠ABN＝30°，AM与BN相交于点C；

(4)取AB的中点G，连结CG；

(5)用量角器量得∠ACB＝______度；

(6)量得CG的长是_____mm，AC的长是_____mm，图中相等的线段有________．

[提示]按语句的顺序，抓住概念用语(如线段、角等)和位置术语(如以……为顶点，在……同侧等)依次画图．

[答案]90，20，20．

AC＝CG＝AG＝BG．