
题目列表(包括答案和解析)
7、抛物线 y=-x2 不具有的性质是( )
A、开口向下 B、对称轴是 y 轴 C、与 y 轴不相交 D、最高点是原点
6、在函数 y= (k<0)的图象上有A(1,y1)、B(-1,
(k<0)的图象上有A(1,y1)、B(-1,
 )、C(-2,
)、C(-2, )三个点,则下列各式中正确( )
)三个点,则下列各式中正确( )
A、y1<y2<y3 B、y1<y3<y2 C、y3<y2<y1 D、y2<y3<y1
5、在直角坐标系中,将矩形OABC沿AC对折,使点B落在点 处,已知
处,已知 ,点
,点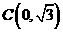 ,则点
,则点 的坐标为( )
的坐标为( )
A、(-,) B、(-,) C、(-,) D、(-,)
4、如图,半圆O的直径AB=4,与半圆O内切的⊙O1与AB切于点M,设⊙O1的半径为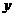 ,AM=
,AM= ,则
,则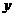 关于
关于 的函数关系式是( )
的函数关系式是( )
A、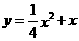 B、
B、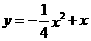 C、
C、 D、
D、
3、已知 y=ax2+bx+c 的图像如图所示,则 a、b、c 满足( )
A、a<0,b<0,c<0 B、a>0,b<0,c>0
C、a<0,b>0,c>0 D、a<0,b<0,c>0
2、弹簧的长度与所挂物体的质量的关系为一次函数,其图象如右图所示,则不挂物体的弹簧长度是( )A、10cm B、8cm C、5cm D、7cm

1、点 P(a,a-2)在第四象限,则 a 的取值范围是( )
A、-2<a<0 B、0<a<2 C、a>2 D、a<0
3.如图,∠AOB是直角,∠AOC等于46°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数.

[提示]
∠MON=∠CON-∠COM.
[答案]
∵ ∠AOB是直角.
∴ ∠AOB=90°(直角的定义),
∵ ∠AOC=46°,
∴ ∠BOC=∠AOB+∠AOC=90°+46°=136°,
∵ ON平分∠BOC,
∴ ∠CON= ∠BOC=
∠BOC= ×136°=68°(角平分线定义),
×136°=68°(角平分线定义),
∵ OM平分∠AOC,
∴ ∠COM= ∠AOC=
∠AOC= ×46°=23°(角平分线定义),
×46°=23°(角平分线定义),
∴ ∠MON=∠CON-∠COM=68°-23°=45°.
答:∠MON=45°.
[点评]
和线段计算一样,在进行有关角度计算时,也要根据已知,仔细看图,找出已知角与所求角的关系,此题中的∠MON还可看成是∠BOM与∠BON的差,∠MON也可看成是∠AOM与∠AON之和,请试一试怎么算,比一比哪种方法较简便.关于角平分线的三种表达式,也应结合图形灵活运用.
2.已知∠a与∠b 互为补角,且∠b 互为补角,且∠b 的 比∠a大15°,求∠a的余角.
比∠a大15°,求∠a的余角.
[提示]
互补两角和为180°,根据题意可知列出关于∠a、∠b的方程组,求出∠a,再根据“互余两角和为90°”,求出∠a的余角.
[答案]
由题意可得:
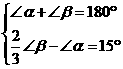
解之得:
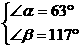
∴ ∠a的余角=90°-∠a=90°-63°=27°.
答:∠a的余角是27°.
1.如图,M是线段AB的中点,点C在线段AB上,且AC=4 cm,N是AC的中点,
MN=3 cm,求线段CM和AB的长.
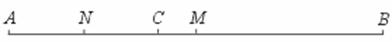
[提示]
CM=MN-NC,AB=2 AM.
[答案]
∵ N是AC中点,AC=4 cm,
∴
NC= AC=
AC= ×4=2(cm),
×4=2(cm),
∵ MN=3 cm,
∴ CM=MN-NC=3-2=1(cm),
∴ AM=AC+CM=4+1=5(cm),
∵ M是AB的中点,
∴ AB=2 AM=2×5=10(cm).
答:线段CM的长为1 cm,AB的长为10 cm.
[点评]
在进行线段的有关计算时,要依据已知,仔细看图,找出已知线段与所求线段的关系,关于线段中点的三种表达方式,应结合图形灵活运用.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com