
题目列表(包括答案和解析)
7.将直线y=2x向上平移两个单位,所得的直线是
A.y=2x+2 B.y=2x-2 C.y=2(x-2) D.y=2(x+2)
6.一次函数y=x+1的图象在( ).
5.下列函数中,一次函数是( ).
(A) (B)
(B) (C)
(C) (D)
(D)
4.若函数 (
( 为常数)的图象如图所示,那么当
为常数)的图象如图所示,那么当 时,
时, 的取值范围是
的取值范围是
A、 B、
B、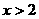 C、
C、 D、
D、
3.阻值为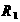 和
和 的两个电阻,其两端电压
的两个电阻,其两端电压 关于电流强度
关于电流强度 的函数图象如图,
的函数图象如图,
则阻值
 (A)
(A)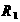 >
> (B)
(B)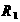 <
< (C)
(C)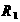 =
= (D)以上均有可能
(D)以上均有可能

2.某市的出租车的收费标准如下:3千米以内的收费6元;3千米到10千米部分每千米加收1.3元;10千米以上的部分每千米加收1.9元。那么出租车收费y(元)与行驶的路程x(千米)之间的函数关系用图象表示为

1.已知一次函数 ,若
,若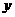 随着
随着 的增大而减小,则该函数图象经过:
的增大而减小,则该函数图象经过:
(A)第一,二,三象限 (B)第一,二,四象限
(C)第二,三,四象限 (D)第一,三,四象限
25.我们做如下的规定:如果一个三角形在运动变化时保持形状和大小不变,则把这样的三角形称为三角形板.
把两块边长为4的等边三角形板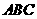 和
和 叠放在一起,使三角形板
叠放在一起,使三角形板 的顶点
的顶点 与三角形板
与三角形板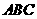 的AC边中点
的AC边中点 重合,把三角形板
重合,把三角形板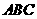 固定不动,让三角形板
固定不动,让三角形板 绕点
绕点 旋转,设射线
旋转,设射线 与射线
与射线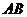 相交于点M,射线
相交于点M,射线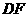 与线段
与线段 相交于点N.
相交于点N.
(1)如图1,当射线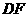 经过点
经过点 ,即点
,即点 与点
与点 重合时,易证△ADM∽△CND.此
重合时,易证△ADM∽△CND.此
时,AM·CN= .
(2)将三角形板 由图1所示的位置绕点
由图1所示的位置绕点 沿逆时针方向旋转,设旋转角为
沿逆时针方向旋转,设旋转角为
 .其中
.其中 ,问AM·CN的值是否改变?说明你的理由.
,问AM·CN的值是否改变?说明你的理由.
(3)在(2)的条件下,设AM= x,两块三角形板重叠面积为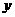 ,求
,求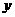 与
与 的函数
的函数
关系式.(图2,图3供解题用)

解:(2)
(3)
以下为草稿纸
24.研究发现,二次函数 (
( )图象上任何一点到定点(0,
)图象上任何一点到定点(0,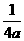 )和到定直线
)和到定直线 的距离相等.我们把定点(0,
的距离相等.我们把定点(0,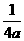 )叫做抛物线
)叫做抛物线 的焦点,定直线
的焦点,定直线 叫做抛物线
叫做抛物线 的准线.
的准线.
(1)写出函数 图象的焦点坐标和准线方程;
图象的焦点坐标和准线方程;
(2)等边三角形OAB的三个顶点都在二次函数 图象上,O为坐标原点,
图象上,O为坐标原点,
求等边三角形的边长;
(3)M为抛物线 上的一个动点,F为抛物线
上的一个动点,F为抛物线 的焦点,P(1,3)
的焦点,P(1,3)
为定点,求MP+MF的最小值.
解:(1)焦点坐标:
准线方程:
(2)
(3)
23.如图,Rt△ABC中,∠C=90°,∠B的平分线交AC于E,DE⊥BE.
(1)试说明AC是△BED外接圆的切线;
 (2)若CE=1,BC=2,求△ABC内切圆的面积.
(2)若CE=1,BC=2,求△ABC内切圆的面积.
解:(1)
(2)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com