
题目列表(包括答案和解析)
8.两圆半径之比为2︰3,当两圆内切时,圆心距是4厘米,当两圆外切时,圆心距为( )
(A)5厘米 (B)11厘米 (C)14厘米 (D)20厘米
[提示]设两圆半径分别为2 x、3 x厘米,则内切时有3 x-2 x=4,所以x=4.于是两圆半径分别为8厘米、12厘米.故外切时圆心距为20厘米.
[答案]D.
[点评]本题考查两圆内切、外切时,圆心距与两圆半径的关系.注意:要理解并记忆两圆的五种位置关系及圆心距与半径的关系.
7.一个扇形的弧长为20p 厘米,面积是240p 厘米2,则扇形的圆心角是……………( )
(A)120° (B)150° (C)210° (D)240°
[提示]设扇形的圆心角为n度,半径为R,则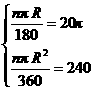 解方程组得
解方程组得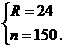
[答案]B.
[点评]本题考查扇形的弧长、面积公式.注意:应熟记扇形的弧长公式、扇形的面积公式.
6.如图,⊙O的弦AB、CD相交于点P,PA=4厘米,PB=3厘米,PC=6厘米,EA切⊙O于点A,AE与CD的延长线交于点E,AE=2 厘米,则PE的长为( )
厘米,则PE的长为( )
(A)4厘米 (B)3厘米 (C)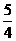 厘米 (D)
厘米 (D) 厘米
厘米

[提示]由相交弦定理,得PA·PB=PD·PC.
∴ 4×3=PD·6.
∴ PD=2(厘米).
由切割线定理,得 AE2=ED·EC.
∴ (2 )2=ED ·(ED+2+6).解此方程得
)2=ED ·(ED+2+6).解此方程得
ED=2或ED=-10(舍去).
∴ PE=2+2=4(厘米).
[答案]A.
[点评]本题考查相交弦定理、切割线定理.注意:应用相交弦定理、切割线定理往往建立方程,通过解方程求解.
5.等边三角形的周长为18,则它的内切圆半径是……………………………………( )
(A)6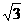 (B)3
(B)3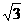 (C)
(C)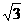 (D)
(D)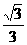
[提示]等边三角形的边长为6,则它的面积为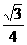 ×62=9
×62=9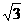 .又因为三角形的面积等于内切圆的半径与三角形的周长的积的一半,所以9
.又因为三角形的面积等于内切圆的半径与三角形的周长的积的一半,所以9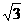 =
=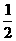 r·18(r为内切圆半径).
r·18(r为内切圆半径).
解此方程,得r=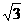 .
.
[答案]C.
[点评]本题考查等边三角形的面积的求法、内切圆半径的求法.注意:求三角形的内切圆的半径,通常用面积法.
4.如图,AB是⊙O的弦,点C是弦AB上一点,且BC︰CA=2︰1,连结OC并延长
交⊙O于D,又DC=2厘米,OC=3厘米,则圆心O到AB的距离为…………( )
(A) 厘米 (B)
厘米 (B)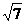 厘米 (C)2厘米 (D)3厘米
厘米 (C)2厘米 (D)3厘米
[提示]延长DO交⊙O于E,过点O作OF⊥AB于F,则CE=8厘米.
 由相交弦定理,得DC·CE=AC·CB,
由相交弦定理,得DC·CE=AC·CB,
所以AC·2 AC=2×8,
故AC=2 (厘米),
(厘米),
从而BC=4 厘米.
厘米.
由垂径定理,得
AF=FB=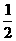 (2
(2 +4
+4 )=3
)=3 (厘米).
(厘米).
所以CF=3 -2
-2 =
= (厘米).
(厘米).
在Rt△COF中,
OF=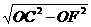 =
=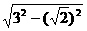 =
=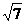 (厘米).
(厘米).
[答案]C.
[点评]本题考查相交弦定理、垂径定理.注意:在圆中求线段的长,往往利用相交弦定理、垂径定理进行线段的转换,再结合勾股定理建立等式.
3.如果正多边形的一个外角等于60°,那么它的边数为……………………………( )
(A)4 (B)5 (C)6 (D)7
[提示]正多边形的外角等于它的中心角,所以 =60°,故n=6.
=60°,故n=6.
[答案]C.
[点评]此题考查正多边形的外角与中心角的关系.注意:正n边形的中心角为 ,且等于它的一个外角.
,且等于它的一个外角.
2.如图,点I为△ABC的内心,点O为△ABC的外心,∠O=140°,则∠I为( )
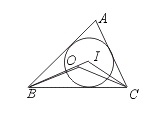 (A)140° (B)125° (C)130° (D)110°
(A)140° (B)125° (C)130° (D)110°
[提示]因点O为△ABC的外心,则∠BOC、∠A分别是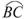 所对的圆心角、圆周角,所以∠O=2∠A,故∠A=
所对的圆心角、圆周角,所以∠O=2∠A,故∠A=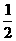 ×140°=70°.又因为I为△ABC的内心,所以
×140°=70°.又因为I为△ABC的内心,所以
∠I=90°+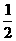 ∠A=90°+
∠A=90°+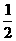 ×70°=125°.
×70°=125°.
[答案]B.
[点评]本题考查圆心角与圆周角的关系,内心、外心的概念.注意三角形的内心与两顶点组成的角与另一角的关系式.
1.有4个命题:
①直径相等的两个圆是等圆;②长度相等的两条弧是等弧;
③圆中最大的弧是过圆心的弧;④一条弦把圆分为两条弧,这两条弧不可能是等弧.
其中真命题是………………………………………………………………………( )
(A)①③ (B)①③④ (C)①④ (D)①
[提示]长度相等的两弧不一定是等弧,故②不对;当弦是直径时,直径把圆分为两个半圆,它们是等弧,故④不对.
[答案]A.[点评]本题考查等圆、等弧、直线与弦的概念.注意:等弧是能互相重合的两条弧,直径是圆中最大的弦.
33. 已知:如图,△ABC是等腰直角三角形,且AD⊥BC,过AD的圆分别交AC、BC、AB于点E、F、G。①求证:GF=AE;②若AB=6,⊙O的半径为
已知:如图,△ABC是等腰直角三角形,且AD⊥BC,过AD的圆分别交AC、BC、AB于点E、F、G。①求证:GF=AE;②若AB=6,⊙O的半径为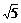 ,求tan∠ADG的值。
,求tan∠ADG的值。
32.如图,AB是⊙O的直径,点P在BA的延长线上,弦CD⊥AB,垂足为E,且PC2=PE·PO。①求证:PC是⊙O的切线;②若OE∶EA=1∶2,PA=16,求⊙O的半径;③在②的条件下,求sin∠PCA的值。
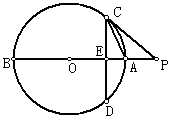
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com