
题目列表(包括答案和解析)
7.已知两圆半径分别为3 cm和7 cm,如果两圆相交,则圆心距 的范围是
,
的范围是
,
如果两圆外离,则圆心距 的范围是
;
的范围是
;
6.已知⊙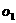 与⊙
与⊙ 的半径分别是3和2,如果它们既不相交又不相切,那么它们的圆心距
的半径分别是3和2,如果它们既不相交又不相切,那么它们的圆心距 的范围是
;
的范围是
;
5.若两园相切,半径分别为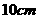 和
和 ,则两园的圆心距的长为
;
,则两园的圆心距的长为
;
4.若两园外切,半径分别为 和
和 ,则其外公切线的长为
;
,则其外公切线的长为
;
3.若两园外切,圆心距为 ,且两园的半径之比为5:3,则大圆的半径为 ,小圆的半径为
;
,且两园的半径之比为5:3,则大圆的半径为 ,小圆的半径为
;
2.两个圆有三条公切线,那么这两个圆的位置关系是 ;
1.两圆的半径分别是 和
和 ,圆心距是
,圆心距是 ,则两圆的位置关心是
;
,则两圆的位置关心是
;
5.(14分)如图,⊙O是以AB为直径的△ABC的外接圆,点D是劣弧 的中点,连
的中点,连
结AD并延长,与过C点的切线交于P,OD与BC相交于点E.(1)求证OE=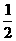 AC;
AC;
*(2)求证: =
= ;(3)当AC=6,AB=10时,求切线PC的长.
;(3)当AC=6,AB=10时,求切线PC的长.
 [提示](1)因为AO=BO,可证OE为△ABC的中位线,可通过证OE∥AC得到OE为中位线;(2)连结CD,则CD=BD,可转化为证明
[提示](1)因为AO=BO,可证OE为△ABC的中位线,可通过证OE∥AC得到OE为中位线;(2)连结CD,则CD=BD,可转化为证明 =
=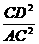 .先证△PCD∽△PAC,得比例式
.先证△PCD∽△PAC,得比例式 =
=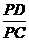 ,两边平方得
,两边平方得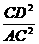 =
=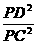 ,再结合切割线定理可证得
,再结合切割线定理可证得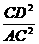 =
= =
= ;(3)利用(2)可求DP、AP,再利用勾股定理、切割线定理可求出PC的长.
;(3)利用(2)可求DP、AP,再利用勾股定理、切割线定理可求出PC的长.
(1)[略证]∵ AB为直径,∴ ∠ACB=90°,
即 AC⊥BC.∵ D为 的中点,由垂径定理,得
的中点,由垂径定理,得
OD⊥BC.∴ OD∥AC.又∵ 点O为AB的中点,∴ 点E为BC的中点.∴ OE=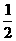 AC.
AC.
*(2)[略证]连结CD.∵ ∠PCD=∠CAP,∠P是公共角,∴ △PCD∽△PAC.∴ 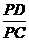 =
= .
.
∴ 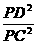 =
=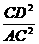 .又 PC是⊙O的切线,∴ PC2=PD·DA.∴
.又 PC是⊙O的切线,∴ PC2=PD·DA.∴  =
=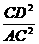 ,
,
∴  =
=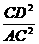 .∵ BD=CD,∴
.∵ BD=CD,∴  =
=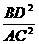 .
.
(3)[略解]在Rt△ABC中,AC=6,AB=10,∴ BC= =8.∴ BE=4.
=8.∴ BE=4.
∵ OE= =3,∴ ED=2.则在Rt△BED中,BD=
=3,∴ ED=2.则在Rt△BED中,BD= =2
=2 ,
,
在Rt△ADB中,AD=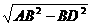 =4
=4 .∵
.∵  =
=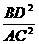 ,∴
,∴  =
= .
.
解此方程,得 PD=5 ,AP=9
,AP=9 .又 PC2=DP·AP,∴ PC=
.又 PC2=DP·AP,∴ PC=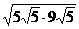 =15.
=15.
29.(12分)已知:如图,⊙O1与⊙O2内切于点P,过点P的直线交⊙O1于点D,交⊙O2于点E;DA与⊙O2相切,切点为C.*(1)求证PC平分∠APD;(2)若PE=3,PA=6,求PC的长.
[提示](1)过点P作两圆的公切线PT,利用弦切角进行角的转换;在(2)题中,可通过证△PCA∽△PEC,得到比例式 =
= ,则可求PC.
,则可求PC.
 *(1)[略证]过点P作两圆的公切线PT,连结CE.∵ ∠TPC=∠4,∠3=∠D.
*(1)[略证]过点P作两圆的公切线PT,连结CE.∵ ∠TPC=∠4,∠3=∠D.
∴ ∠4=∠D+∠5,∴ ∠2+∠3=∠D+∠5.∴ ∠2=∠5.
∵ DA与⊙O相切于点C,∴ ∠5=∠1.∴ ∠1=∠2.即PC平分∠APD.
(2)[解]∵ DA与⊙O2相切于点C,∴ ∠PCA=∠4.
由(1),可知∠2=∠1.∴ △PCA∽△PEC.
∴  =
= .即 PC2=PA·PE.∵ PE=3,PA=6,∴ PC2=18.∴ PC=3
.即 PC2=PA·PE.∵ PE=3,PA=6,∴ PC2=18.∴ PC=3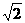 .
.
28.(8分)如图,已知ABCD是圆内接四边形,EB是⊙O的直径,且EB⊥AD,AD与BC的延长线交于F,求证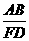 =
= .
.
 [提示]连结AC,证△ABC∽△FDC.显然∠FDC=∠ABC.因为AD⊥直径EB,由垂径定理得
[提示]连结AC,证△ABC∽△FDC.显然∠FDC=∠ABC.因为AD⊥直径EB,由垂径定理得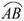 =
=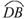 ,故∠DAB=∠ACB.又因为∠FCD=∠DAB,所以
,故∠DAB=∠ACB.又因为∠FCD=∠DAB,所以
∠FCD=∠ACB,故△ABC∽△FDC,则可得出待证的比例式.
[略证]连结AC.∵ AD⊥EB,且EB为直径,∴ 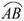 =
=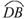 .
.
∴ ∠ACB=∠DAB.∵ ABCD为圆内接四边形,∴ ∠FCD=∠DAB,∠FDC=∠ABC.
∴ ∠ACB=∠FCD.∴ △ABC∽△FDC.∴ 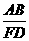 =
= .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com