26．已知：如图，F是四边形ABCD对角线AC上一点，EF∥BC，FG∥AD．

求证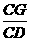：+＝1．

[提示]利用AC＝AF+FC．

[答案]∵　EF∥BC，FG∥AD，

∴　＝，＝．

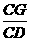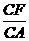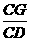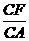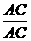∴　+＝+＝＝1．

25．如图，在△ABC中，AB＝AC，延长BC至D，使得CD＝BC，CE⊥BD交AD于E，连结BE交AC于F，求证AF＝FC．

[提示]先证△BCF∽△DBA，再证＝．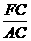

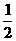[答案]∵　BC＝CD，EC⊥BD，

∴　BE＝DE，∠FBC＝∠D．

又　AB＝AC，

∴　∠BCF＝∠DBA．

∴　∠BCF∽△DBA．

∴　＝．

又　BD＝2BC，AB＝AC，

∴　＝＝．

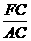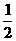∴　FC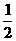＝AC．

因此　AF＝FC．

24．如图，△ABC中，CD⊥AB于D，E为BC中点，延长AC、DE相交于点F，

求证＝．

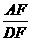[提示]过F点作FG∥CB，只需再证GF＝DF．

[答案]方法一：作FG∥BC交AB延长线于点G．

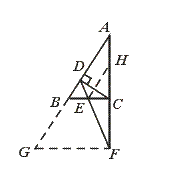∵　BC∥GF，

∴　＝．

又　∠BDC＝90°，BE＝EC，

∴　BE＝DE．

∵　BE∥GF，

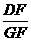∴　＝＝1．

∴　DF＝GF．

∴　＝．

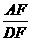方法二：作EH∥AB交AC于点H．

∵　＝，＝，

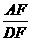∠BDC＝90°，BE＝EC，

∴　BE＝DE．

∴　＝．

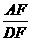23．方格纸中，每个小格的顶点叫做格点，以格点连线为边的三角形叫做格点三角形．请你在图示的10×10的方格纸中，画出两个相似但不全等的格点三角形，并加以证明(要求所画三角形是钝角三角形，并标明相应字母)．

[提示]先任意画一个格点钝角三角形，然后三边都扩大相同的倍数，画出另一个格点钝角三角形．

22．如图，已知AD∥EF∥BC，且AE＝2EB，AD＝8 cm，AD＝8 cm，BC＝14 cm，

则S_梯形AEFD︰S_梯形BCFE＝____________．

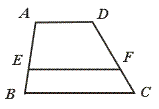
[提示]延长EA，与CD的延长线交于P点，则△APD∽△EPF∽△BPC．

[答案]．

21．如图，直角梯形ABCD中，AD∥BC，AC⊥AB，AD＝8，BC＝10，则梯形ABCD面积是_________．

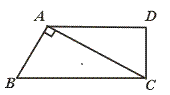
[提示]作AE∥DC交BC于E点，由Rt△ABE∽Rt△CBA，依次算出BE、AB的长，最后求出AE的长，即可求出梯形面积．

[答案]36．

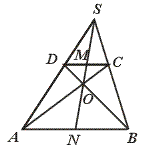
20．如图，△ABC中，AB＝AC，AD⊥BC于D，AE＝EC，AD＝18，BE＝15，则

△ABC的面积是______．

[提示]作EF∥BC交AD于F．设BE交AD于O点，先求出OD长和OB长，最后用勾股定理求出BD的长．

[答案]144．

19．如图，AD是△ABC的角平分线，DE∥AC，EF∥BC，AB＝15，AF＝4，则DE的长等于________．

[提示]DE＝AE，CF＝DE，并考虑＝．

[答案]6．

18．如图，已知△ABC，P是AB上一点，连结CP，要使△ACP∽△ABC，只需添加条件______(只要写出一种合适的条件)．

[提示]∵　∠A为公共角，

∴　考虑∠A的两边或其他内角相等．

[答案]∠B＝∠ACP，或∠ACB＝∠APC，或AC²＝AP·AB．

17．如图，AB∥CD，图中共有____对相似三角形．

[提示]分“”类和“”类两类．

[答案]6对．