
题目列表(包括答案和解析)
6.已知:如图,∠ADE=∠ACD=∠ABC,图中相似三角形共有………………( )
(A)1对 (B)2对 (C)3对 (D)4对

[提示]分别把CD、DE擦去,考察△ADE和△ABC、△ACD和△ABC的关系.[答案]C.
[点评]本题要求运用三角形相似的基本定理与判定定理的运用.
5.如图,在Rt△ABC中,CD是斜边AB上的高,则图中的相似三角形共有………( )

(A)1对 (B)2对 (C)3对 (D)4对
[提示]考虑Rt△ABC与Rt△ACD和Rt△CBD相似情况.
[答案]C.
[点评]本题要求运用直角三角形被斜边上的高所分割成两个直角三角形这种基本图形.
4.下列判断中,正确的是………………………………………………………………( )
(A)各有一个角是67°的两个等腰三角形相似
(B)邻边之比都为2︰1的两个等腰三角形相似
(C)各有一个角是45°的两个等腰三角形相似
(D)邻边之比都为2︰3的两个等腰三角形相似
[提示]设计出反例淘汰错误的选项.[答案]B.
[点评]本题要求运用相似三角形的判定定理.A不成立的原因是当底角为67°时,顶角为46°,另一个三角形的顶角为67°时,底角为66.5°,这两个等腰三角形不相似.C不成立的原因也是顶角不等.D不成立的原因是当一个等腰三角形的腰与底的比是2︰3时,另一个等腰三角形的腰与底的比为3︰2,它们三边之比分别为2︰2︰3与3︰3︰2.
3.如图,DE∥BC,在下列比例式中,不能成立的是………………………………( )

(A) =
= (B)
(B)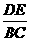 =
= (C)
(C)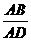 =
= (D)
(D) =
=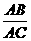
[提示]用特殊值法来筛选出选项,D、E分别为AB、AC的中点,计算每个线段比.[答案]B.
[点评]本题要求运用平行线分线段成比例定理和三角形一边平行线的性质定理,选B的原因是,当E为AC的中点时, =1,D为AB的中点,
=1,D为AB的中点, =
= .
.
2.已知线段d是线段a、b、c的第四比例项,其中a=2 cm,b=4 cm,c=5 cm,则d等于……( )
(A)1 cm(B)10 cm(C)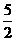 cm(D)
cm(D) cm.
cm.
[提示]列出比例式:a︰b=c︰d,解出d.[答案]B.
[点评]本题要求运用比例的概念和求第四比例项的基本方法.
1.已知5y-4x=0,那么(x+y)︰(x-y)的值等于………………………………( )
(A) (B)-9 (C)9 (D)-
(B)-9 (C)9 (D)-
[提示]将5y-4x=0改写成 =
=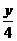 ,用比例性质得
,用比例性质得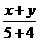 =
= .[答案]C.
.[答案]C.
[点评]本题要求运用比例性质进行计算.
30.如图,在Rt△ABC中,∠C=90°,BC=6 cm,CA=8 cm,动点P从点C出
发,以每秒2 cm的速度沿CA、AB运动到点B,则从C点出发多少秒时,可使
S△BCP=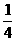 S△ABC?
S△ABC?
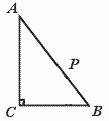
[提示]先求CP,再求DP.
[答案]当点P从点C出发,运动在CA上时,若S△BCP=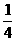 S△ABC,则
S△ABC,则
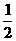 ·CP·BC=
·CP·BC=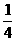 ·
·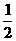 AC·BC,
AC·BC,
∴ CP=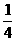 ·AC=2(cm).
·AC=2(cm).
故由点P的运动速度为每秒2 cm,它从C点出发1秒时,有S△BCP=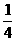 S△ABC.当点P从点C出发运动到AB上时,如图,可过点P作PD⊥BC于D.
S△ABC.当点P从点C出发运动到AB上时,如图,可过点P作PD⊥BC于D.
若S△BCP=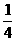 S△ABC,则
S△ABC,则

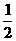 PD·BC=
PD·BC=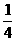 ·
·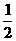 AC·BC.
AC·BC.
∴ PD=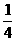 AC=2(cm).
AC=2(cm).
∵ Rt△BAC∽Rt△BPD,
∴ 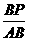 =
= .
.
又 AB=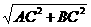 =10,
=10,
故 BP= =
= ,AP=AB-BP=10-
,AP=AB-BP=10- =7.5.
=7.5.
也就是说,点P从C出发共行15.5 cm,用去7.75秒,此时S△BCP=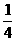 S△ABC.
S△ABC.
答:1秒或7.75秒.
29.如图,在矩形ABCD中,E为AD的中点,EF⊥EC交AB于F,连结FC
(AB>AE).
(1)△AEF与△EFC是否相似?若相似,证明你的结论;若不相似,请说明理由;
(2)设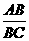 =k,是否存在这样的k值,使得△AEF∽△BFC,若存在,证明你的结论并求出k的值;若不存在,说明理由.
=k,是否存在这样的k值,使得△AEF∽△BFC,若存在,证明你的结论并求出k的值;若不存在,说明理由.

[提示](1)如图,证明△AFE≌△DGE,证出∠AFE=∠EFC.
(2)证明∠ECG=30°,∠BCF=30°.
[答案]如图,是相似.

[证明]延长FE,与CD的延长线交于点G.
在Rt△AEF与Rt△DEG中,
∵ E是AD的中点,
∴ AE=ED.
∵ ∠AEF=∠DEG,
∴ △AFE≌△DGE.
∴ ∠AFE=∠DGE.
∴ E为FG的中点.
又 CE⊥FG,
∴ FC=GC.
∴ ∠CFE=∠G.
∴ ∠AFE=∠EFC.
又 △AEF与△EFC均为直角三角形,
∴ △AEF∽△EFC.
① 存在.如果∠BCF=∠AEF,即k=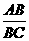 =
=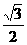 时,△AEF∽△BCF.
时,△AEF∽△BCF.
证明:当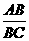 =
=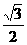 时,
时, =
= ,
,
∴ ∠ECG=30°.
∴ ∠ECG=∠ECF=∠AEF=30°.
∴ ∠BCF=90°-60°=30°.
又 △AEF和△BCF均为直角三角形,
∴ △AEF∽△BCF.
② 因为EF不平行于BC,
∴ ∠BCF≠∠AFE.
∴ 不存在第二种相似情况.
28.如图,∠ABC=∠CDB=90°,AC=a,BC=b.
(1)当BD与a、b之间满足怎样的关系时,△ABC∽△CDB?
(2)过A作BD的垂线,与DB的延长线交于点E,若△ABC∽△CDB.
求证四边形AEDC为矩形(自己完成图形).

[提示]利用三角形相似,推出BD= .
.
[答案](1)∵ ∠ABC=∠CDB=90°,
∴ 当 =
= 时,△ABC∽△CDB.
时,△ABC∽△CDB.
即 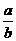 =
= .
.
∴ BD= .
.
即当BD= 时,△ABC∽△CDB.
时,△ABC∽△CDB.
∵ △ABC∽△CDB,
∴ ∠ACB=∠CBD.
∴ AC∥ED.
又 ∠D=90°,
∴ ∠ACD=90°.
∴ ∠E=90°.
∴ 四边形AEDC为矩形.
27.如图,BD、CE分别是△ABC的两边上的高,过D作DG⊥BC于G,分别交CE及BA的延长线于F、H,求证:
(1)DG2=BG·CG;(2)BG·CG=GF·GH.

[提示](1)证△BCG∽△DCG;(2)证Rt△HBG∽Rt△CFG.
[答案](1)DG为Rt△BCD斜边上的高,
∴ Rt△BDG∽Rt△DCG.
∴ 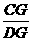 =
=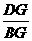 ,即DG2=BG·CG.
,即DG2=BG·CG.
(2)∵ DG⊥BC,
∴ ∠ABC+∠H=90°,CE⊥AB.
∴ ∠ABC+∠ECB=90°.
∴ ∠ABC+∠H=∠ABC+∠ECB.
∴ ∠H=∠ECB.
又 ∠HGB=∠FGC=90°,
∴ Rt△HBG∽Rt△CFG.
∴ 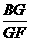 =
= ,
,
∴ BG·GC=GF·GH.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com