
题目列表(包括答案和解析)
27、(本题满分8分)已知:抛物线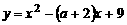 的顶点在坐标轴上.
的顶点在坐标轴上.
(1)求a的值;
(2)若该抛物线的顶点C在x轴的正半轴上,而此抛物线与直线y=x+9交于A、B两点,且A点在B点左侧,P为线段AB上的点(A、B两端点除外). 过点P作x轴的垂线与抛物线交于点Q.(可在题中给出的坐标系内画示意图)
问:①线段AB上是否存在这样的点P,使得PQ的长等于6?若存在,请求出点P的坐标;若不存在,请说明理由.
 ②线段AB上是否存在这样的点P,使得△ABQ∽△OAC?若存在,请求出此时点Q的坐标;若不存在,请说明理由.
②线段AB上是否存在这样的点P,使得△ABQ∽△OAC?若存在,请求出此时点Q的坐标;若不存在,请说明理由.
26、(本题满分8分)某市部分初三学生参加了2004年全国初中数学竞赛决赛,并取得优异成绩. 已知竞赛成绩分数都是整数,试题满分为140分. 现随机抽样统计300名参赛学生的成绩分数分布情况如下:
|
分数段 |
0-19 |
20-39 |
40-59 |
60-79 |
80-99 |
100-119 |
120-139 |
|
人数 |
0 |
37 |
68 |
95 |
58 |
30 |
12 |
请根据以上信息解答下列问题:
(1)经竞赛组委会评定,竞赛成绩在100分以上(含100分)的考生均可获得不同等级的奖励,试估计该市参加本次数学竞赛决赛考生的获奖比例;
(2)你认为该市本次决赛成绩分数的中位数最有可能落在哪个分数段内?
(3)上表还提供了其他信息,例如:“样本中获奖的人数为42人”等等,请你再写出两条此表提供的信息;
(4)若某同学平时数学学习成绩一直都处于班级前3名(所在班级人数50人),在本次数学竞赛中,他未得奖. 这属于哪一类事件?(可能事件、不可能事件、必然事件)
25、(本题满分8分)某水果批发商场经销一种高档水果,如果每千克盈利10元,每天可售出500千克. 经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6000元,同时又要顾客得到实惠,那么每千克应涨价多少元?
(2)若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?
24、(本题满分5分)某校厨房有一太阳能热水器,其水箱的最大蓄水量为1200升.已知水箱的蓄水量y(升)与注水时间x(分钟)之间有如下关系:
|
x(分钟) |
0 |
2 |
4 |
6 |
… |
|
y(升) |
0 |
80 |
160 |
240 |
… |
(1)根据上表中的数据,在上图的坐标系中描出相应的各点,顺次连结各点后,根据图象试猜想水箱的蓄水量y(升)与注水时间x(分钟)之间的函数解析式;
(2)请验证上表中各点的坐标是否满足这个函数解析式,归纳你的结论,并写出自变量x的取值范围.
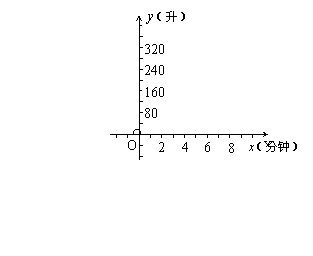
23、(本题满分6分)在如图的方格纸中(每个小方格的边长都是1个单位)有一点O和△ABC.
(1)请以点O为位似中心,把△ABC缩小为原来的一半(不改变方向),得到△A′B′C′.
 (2)请用适当的方式描述△A′B′C′的顶点A′、B′、C′的位置.
(2)请用适当的方式描述△A′B′C′的顶点A′、B′、C′的位置.
22、(本题共有2小题,每小题4分,共8分)
 (1)如图,在□ABCD中,对角线AC、BD相交于点O. 请找出图中的一对全等三角形,并给予证明.
(1)如图,在□ABCD中,对角线AC、BD相交于点O. 请找出图中的一对全等三角形,并给予证明.
(2)规定:一条弧所对的圆心角的度数作为这条弧的度数.
 ①如图,在⊙O中,弦AC、BD相交于点P,已知弧AB、弧CD分别为65°和45°,则∠APB= °;(友情提示:连结AD试一试)
①如图,在⊙O中,弦AC、BD相交于点P,已知弧AB、弧CD分别为65°和45°,则∠APB= °;(友情提示:连结AD试一试)
②一般地,在⊙O中,弦AC、BD相交于点P,若弧AB、弧CD分别为m°和n°,则∠APB= °(用m、n的代数式表示).
21、(本题共有3小题,每小题5分,共15分)
(1)解方程: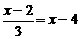 (2)解不等式
(2)解不等式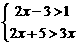
(3)先将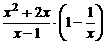 化简,然后请自选一个你喜欢的x值,再求原式的值.
化简,然后请自选一个你喜欢的x值,再求原式的值.
20、 在圆环形路上有均匀分布的四家工厂甲、乙、丙、丁,每家工厂都有足够的仓库供产品储存. 现要将所有产品集中到一家工厂的仓库储存,已知甲、乙、丙、丁四家工厂的产量之比为1∶2∶3∶5. 若运费与路程、运的数量成正比例,为使选定的工厂仓库储存所有产品时总的运费最省,应选的工厂是( )
在圆环形路上有均匀分布的四家工厂甲、乙、丙、丁,每家工厂都有足够的仓库供产品储存. 现要将所有产品集中到一家工厂的仓库储存,已知甲、乙、丙、丁四家工厂的产量之比为1∶2∶3∶5. 若运费与路程、运的数量成正比例,为使选定的工厂仓库储存所有产品时总的运费最省,应选的工厂是( )
A、甲 B、乙 C、丙 D、丁
19、某村的粮食总产量为a(a为常量)吨,设该村粮食的人均产量为y(吨),人口数为x,则y与x之间的函数图象应为图中的( )

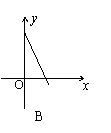


18、在一副52张扑克牌中(没有大小王)任意抽取一张牌,抽出的这张牌是方块的机会是( )
A、 B、
B、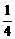 C、
C、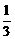 D、0
D、0
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com