2．计算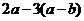的结果是(　)

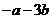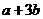A．　　　　　　　 B．　　　　　　　　 C．　　　　　　　　 D．

1．4的算术平方根是(　)

A．　　　　　　　　　 B．　　　　　　　　 C．　　　　　　　 D．

30、(本小题满分12分)

如图，平面直角坐标系中，四边形OABC为矩形，点A、B的坐标分别为(6，0)，(6，8)。动点M、N分别从O、B同时出发，以每秒1个单位的速度运动。其中，点M沿OA向终点A运动，点N沿BC向终点C运动。过点N作NP⊥BC，交AC于P，连结MP。已知动点运动了x秒。

(1)P点的坐标为(　 　　　　　　，　　　　　　　 )；(用含x的代数式表示)

(2)试求 ⊿MPA面积的最大值，并求此时x的值。

(3)请你探索：当x为何值时，⊿MPA是一个等腰三角形？

你发现了几种情况？写出你的研究成果。

29、(本小题满分10分)

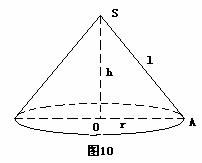已知圆锥的底面半径为r＝20cm，高h=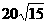cm,现在有一只蚂蚁从底边上一点A出发。在侧面上爬行一周又回到A点，求蚂蚁爬行的最短距离。

28、(本小题满分10分)

集市上有一个人在设摊“摸彩”，只见他手拿一个黑色的袋子，内装大小、形状、质量完全相同的白球20只，且每一个球上都写有号码(1－20号)和1只红球，规定：每次只摸一只球。摸前交1元钱且在1--20内写一个号码，摸到红球奖5元，摸到号码数与你写的号码相同奖10元。

(1)　　　 你认为该游戏对“摸彩”者有利吗？说明你的理由。

(2)　　　 若一个“摸彩”者多次摸奖后，他平均每次将获利或损失多少元？

27、(本小题满分10分)

某地区为了加大“退耕还林”的力度，出台了一系列的激励措施：在“退耕还林”过程中，每一年的林地面积达到10亩且每年的林地面积在增加的农户，当年都可得生活补贴费2000元，且每超过10亩的部分还给予奖励每亩a元，在林间还有套种其他农作物，平均每亩还有b元的收入。

下表是某农户在头两年通过“退耕还林”每年获得的总收入情况：

(注：年总收入＝生活补贴量+政府奖励量+种农作物收入)

(1)　　　 试根据以上提供的资料确定a、b的值。

(2)　　　 从2003年起，如果该农户每年新增林地的亩数比前一年按相同的增长率增长，那么2005年该农户获得的总收入达到多少元？

26、(本小题满分8分)

在平面直角坐标系中，圆心O的坐标为(-3，4)，以半径r在坐标平面内作圆，

(1)当r　　　　　　 时，圆O与坐标轴有1个交点；

(2)当r　　　　　　 时，圆O与坐标轴有2个交点；

(3)当r　　　　　　 时，圆O与坐标轴有3个交点；

(4)当r　　　　　　 时，圆O与坐标轴有4个交点；

25、(本题满分8分)

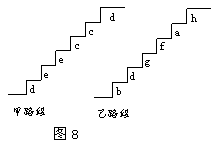同学：你去过黄山吗？在黄山的上山路上，有一些断断续续的台阶，如图8是其中的甲、乙段台阶路的示意图， 图8中的数字表示每一级台阶的高度(单位:cm).并且数d,e,e,c,c,d的方差p,数据b,d,g,f,a,h的方差q，(10cm＜a＜b＜c＜d＜e＜f＜g＜h＜20cm,且 p＜q)，请你用所学过的有关统计知识(平均数、中位数、方差和极差)回答下列问题：

(1)两段台阶路有哪些相同点和不同点？

(2)哪段台阶路走起来更舒服？为什么？

(3)为方便游客行走，需要重新整修上山的小路.对于这两段台阶路，在台阶数不变的情况下，请你提出合理的整修建议.

24、(本小题满分6分)

　 已知抛物线与x轴交于A(－1，0)和B(3，0)两点，且与y轴交于点C(0，3)。

(1)求抛物线的解析式；(2)抛物线的对称轴方程和顶点M坐标；(3)求四边形ABMC的面积。

23、(本小题满分6分)

观察下面的点阵图，探究其中的规律。

摆第1个“小屋子”需要5个点，

摆第2个“小屋子”需要　　　 个点，摆第3个“小屋子”需要　　　　　 个点？(1)、摆第10个这样的“小屋子”需要多少个点？　　　 图7

(2)、写出摆第n个这样的“小屋子”需要的总点数，S与n的关系式。