6、如图，一宽为2cm的刻度尺在圆上移动，当刻度尺的一边与圆相切时，另一边与圆两个交点处的读数恰好为“1”和“4”(单位：cm)，则该圆的半径为(　　　 )

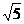A．5cm　 B．cm　 C．cm D．cm

5、甲、乙两同学从A地出发，骑自行车在同一条路上行驶到B地，他们离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系的图象如图6所示，根据图中提供的信息，有下列说法：

(1)他们都行驶了18千米；

(2)甲在途中停留了0.5小时；

(3)乙比甲晚出发了0.5小时；

(4)相遇后，甲的速度小于乙的速度；

(5)甲、乙两人同时到达目的地．

其中，符合图象描述的说法有(　　 )

A．2个　　　　　 B．3个　　　　　 C．4个　　　　　 D．5个

4、观察右表中数字的排列规律，回答下面的问题:①表中第1行第5列的数字是　　　　 ；②表中第5行第4列的数字是　　　　 ；③请用关于n的代数式表示表中第3列第n行的数为　　　　　　 ；④数字2006的位置是第　　　 行，第　　　 列．

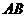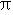3、如图，将半径为2cm的⊙O分割成十个区域，其中弦、关于点对称，、关于点对称，连结，则图中阴影部分的面积是__　cm(结果用表示)．

2、如图，一牧童在A处牧马，牧童家在B处，A，B处距河岸的距离AC，BD分别为500m和700m，且CD=500m，天黑前牧童从A处将马赶到河边去饮水后再回家，那么牧童最少要走__________m．

1、如图，正方形ABCD的边长为8，M在DC上，且DM=2，N是AC上一动点，则DN+MN的最小值为　　　 .

第1题图　　　　 第2题图　　　　　 第3题图　　　　　　 第6题图

13、如图，Rt△AOB是一张放在平面直角坐标系中的三角形纸片，点O与原点重合，点A在x轴上，点B在y轴上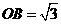，，∠BAO＝30°，将Rt△AOB折叠，使OB边落在AB边上，点O与点D重合，折痕为BE。

⑴求点E和点D的坐标；

⑵求经过O、D、A三点的二次函数解析式；

⑶设直线BE与⑵中二次函数图象的对称轴交于点F，M为OF中点，N为AF中点，在x轴上是否存在点P，使△PMN的周长最小，若存在，请求出点P的坐标和最小值；若不存在，请说明理由。

12、已知，如图，直角坐标系中的等腰梯形ABCD，AB∥CD，下底AB在x轴上，D在y轴上，M为AD的中点，过O作腰BC的垂线交BC于点E.

(1)求证：OM⊥OE；

(2)若等腰梯形中AD所在的直线的解析式为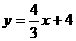，且，求过等腰梯形ABCD的三个顶点的抛物线的解析式。

(3)若点M在梯形ABCD内沿水平方向移动到N，且使四边形MNCD为平行四边形，抛物线上是否存在一点P，使S_△PAB与四边形MNCD的面积相等，若存在，求出P点的坐标；若不存在，请说明理由。

11、如图，在Rt△AOB中，∠AOB=90°，OA=3cm，OB=4cm，以点O为坐标原点建立坐标系，设P、Q分别为AB、OB边上的动点它们同时分别从点A、O向B点匀速运动，速度均为1cm/秒，设P、Q移动时间为t(0≤t≤4)

(1)过点P做PM⊥OA于M，求证：AM：AO=PM：BO=AP：AB，并求出P点的坐标(用t表示)

(2)求△OPQ面积S(cm²)，与运动时间t(秒)之间的函数关系式，当t为何值时，S有最大值？最大是多少？

(3)当t为何值时，△OPQ为直角三角形？

(4)证明无论t为何值时，△OPQ都不可能为正三角形。若点P运动速度不变改变Q 的运动速度，使△OPQ为正三角形，求Q点运动的速度和此时t的值。

10、在某张航海图上，标明了三个观测点的坐标为O(0，0)、B(12，0)、C(12，16)，由三个观测点确定的圆形区域是海洋生物保护区，如图所示．

(1)求圆形区域的面积(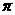取3.14)；

(2)某时刻海面上出现一渔船A，在观测点O测得A位于北偏东45°方向上，同时在观测点B测得A位于北偏东30°方向上，求观测点B到渔船A的距离(结果保留三个有效数字)；

(3)当渔船A由(2)中的位置向正西方向航行时，是否会进入海洋生物保护区？请通过计算解释．