5．已知，如图，点C为线段AB上一点，△ACM，△CBN是等边三角形，则图(1)中存在结论AN=BM

(1)现将△ACM绕C点按逆时针方向旋转180⁰，使A点落在CB上，请在画出符合题意的图(2)

(2)在(2)中所得的图形中，结论“AN=BM”是否还成立？若成立，请证明；若不成立，请说明理由

(3)在(2)得到的图形中，设MA的延长线与BN相交于D点，请你判断△ABD与四边形MDNC的形状，并证明你的结论

4．如图，AD是⊙O的直径，BC切⊙O于D，AB，AC交⊙O于E，F

(1)求证：AE·AB=AF·AC

(2)如果将直线BC向上或向下平移(与AD仍然垂直)且AB，AC交⊙O于E，F，则AE·AB=AF·AC还成立吗？

3．如图，课本中曾要我们证明“已知平行四边形ABCD及形舛一直线L，AA₁⊥L，BB₁⊥L，CC₁⊥L，DD₁⊥L。求证：AA₁+CC₁=BB₁+DD₁”。现将L向上平移，则以上的结论还成立吗？

2．如图，已知AB是⊙O的直径，直线MN与⊙O相交于点E，F，AD⊥MN，垂足为D。

(1)求证：∠BAE=∠DAF

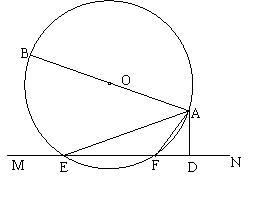(2)若把直线MN向上平行移动，使之与AB相交，其他条件不变，请把变化后图形画出来，并指出∠BAE=∠DAF是否仍然相等(直接回答，不必证明)

1．如图，已知⊙O₁经过⊙O₂的圆心O₂，且与⊙O₂相交于A、B两点，点C为弧AO₂B上的一动点(不运动至A、B)，连结AC，并延长交⊙O₂于点P，连结BP、PC

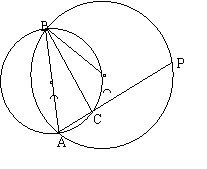(1)当点C在运动时，观察图中有哪些角的大小没有变化？

(2)请猜想△BCP的形状，并证明你的猜想

29．(本题满分10分)

如图，正方形ABCD的边长为12，划分成12×12个

小正方形. 将边长为n(n为整数，且2≤n≤11)的黑白

两色正方形纸片按图中的方式黑白相间地摆放，第一张

n×n的纸片正好盖住正方形ABCD左上角的n×n个小正

方形格，第二张纸片盖住第一张纸片的部分恰好为(n－1)

×(n－1)的正方形. 如此摆放下去，最后直到纸片盖住

正方形ABCD的右下角为止. 请你认真观察思考后回答下

列问题：

(1)由于正方形纸片边长n的取值不同，完成摆放时所使用正方形纸 片的张数也不同，请填写下表：

(2)设正方形ABCD被纸片盖住的面积(重合部分只计一次)为S₁，未被盖住的面积为S₂.

①当n=2时，求S₁∶S₂的值；

②是否存在使得S₁=S₂的n值？若存在，请求出这样的n值；若不存在，请说明理由.

28．(本题满分8分)

如图，在平面直角坐标系中，直线l的解析式为y=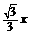，关于x的一元二次方程

2x²－2(m+2)x+2m+5=0(m>0)有两个相等的实数根.

(1)试求出m的值，并求出经过点A(0，－m)和点D(m，0)的直线解析式；

(2)在线段AD上顺次取两B、C，使AB=CD=－1，试判断ΔOBC的形状；

(3)设直线l与直线AD交于点P，图中是否存在与ΔOAB相似的三角形？如果存在，请直接写出来；如果不存在，请说明理由.

27．(本题满分9分)

某生活小区的居民筹集资金1600元，计划在一块上、下底分别为10cm，20cm的梯形空地上种植花木(如图).

(1)他们在ΔAMD和ΔBMC地带上种植太阳花，单价为8元/cm²，当ΔAMD地带种满花后(图中阴影部分)共花了160元，请计算种满ΔBMC地带所需的费用；

(2)若其余地带要种的有玫瑰和茉莉花两种花木可供选择，单价分别为12元/cm²和10元/cm²，应选择种那种花木，刚好用完所筹集资金？

(3)若梯形ABCD为等腰梯形，面积不变(如图)，请你设计一种花坛图案，即在梯形内找到一点P，使得ΔAPB≌ΔDPC，且S_ΔAPD=S_ΔBPC，，并说出你的理由.

26．(本题满分8分)

如图是某段河床横断面的示意图. 查阅该河段的水文资料，得到下表中的数据：

x(cm)	5	10	20	30	40	50
y(cm)	0.125	0.5	2	4.5	8	12.5

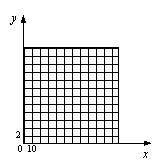
(1)请你以上表中的各对数据(x，y)作为点的坐标，

尝试在下面所给的坐标系中画出y关于x的函数图像；

(2)①填写下表：

②根据所填表中数据呈现的规律，猜想出用x表示y的二次函数关系式：___________;

(3)当水面宽度为36m时，一艘吃水深度(船底部到水面的距离)为1.8m的货船能

否在这个河段安全通过？为什么？

25．(本题满分6分)

如图，有两个可以自由转动的均匀转盘A、B，转盘A被均匀地分成4等分，每份分别

标上1，2，3，4四个数字；转盘B被均匀地分成6等份，每份分别标上1，2，3，4，5，6六个数字. 有人为甲、乙两人设计了一个游戏，其规则如下：

(1)同时自由转动转盘A、B；

(2)转盘停止后，指针各指向一个数字(如果指针恰好指在分格线上，那么重转一次，

直到指针指向某一数字为止)，用所指的两个数字作成积. 如果得到的积是偶数，那么甲胜；如果得到的积是奇数，则乙胜(如果转盘A指针指向3，转盘B指针指向5，3×5=15，按规则乙胜).

你认为这样的规则是否公平？请说明理由；如果不公平，请你设计一个公平的规则，并

说明理由.