
题目列表(包括答案和解析)
2.将五张分别画有等边三角形、平行四边形、矩形、等腰梯形、正六边形的卡片任意摆放,将有图形的一面朝下,从中任意翻开一张卡片,图形一定是中心对称图形的概率是( )
(A)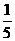 (B)
(B) (C)
(C) (D)
(D)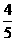
1.我市某一周的最高气温统计如下表:
|
最高气温(℃) |
25 |
26 |
27 |
28 |
|
天数 |
1 |
1 |
2 |
3 |
则这组数据的中位数与众数分别是( )
(A)27,28 (B)27.5,28
(C)28,27 (D)26.5,27
4.在具体情境中了解概率的意义;能够运用列举法(包括列表、画树状图)求简单事件发生的概率.能够准确区分确定事件与不确定事件.
3.能够对扇形统计图、列频数分布表、画频数分布直方图和频数折线图等几种统计图表进行具体运用,并会根据实际情况对统计图表进行取舍,
2.了解总体、个体、样本、平均数、加权平均数、中位数、众数、极差、方差、频数、频率等概念,并能进行有效的解答或计算.
6.已知一元二次方程 的两个根满足
的两个根满足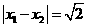 ,且a,b,c分别是
,且a,b,c分别是 的∠A,∠B,∠C的对边.若
的∠A,∠B,∠C的对边.若 ,求∠B的度数.小敏解得此题的正确答案“
,求∠B的度数.小敏解得此题的正确答案“ ”后,思考以下问题,请你帮助解答.
”后,思考以下问题,请你帮助解答.
(1)若在原题中,将方程改为 ,要得到
,要得到 ,而条件“
,而条件“ ”不变,那么对应条件中的
”不变,那么对应条件中的 的值作怎样的改变?并说明理由.
的值作怎样的改变?并说明理由.
(2)若在原题中,将方程改为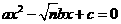 (n为正整数,
(n为正整数, ),要得到
),要得到 ,而条件“
,而条件“ ”不变,那么条件中的
”不变,那么条件中的 的值应改为多少(不必说明理由)?
的值应改为多少(不必说明理由)?
5.青青商场经销甲、乙两种商品,甲种商品每件进价15元,售价20元;乙种商品每件进价35元,售价45元.
(1)若该商场同时购进甲、乙两种商品共100件恰好用去2 700元,求能购进甲、乙两种商品各多少件?
(2)该商场为使甲、乙两种商品共100件的总利润(利润=售价-进价)不少于750元,且不超过760元,请你帮助该商场设计相应的进货方案;
(3)在“五·一”黄金周期间,该商场对甲、乙两种商品进行如下优惠促销活动:
|
打折前一次性购物总金额 |
优惠措施 |
|
不超过300元 |
不优惠 |
|
超过300元且不超过400元 |
售价打九折 |
|
超过400元 |
售价打八折 |
按上述优惠条件,若小王第一天只购买甲种商品一次性付款200元,第二天只购买乙种商品打折后一次性付款324元,那么这两天他在该商场购买甲、乙两种商品一共多少件?(通过计算求出所有符合要求的结果)
4.如图19,设抛物线 交x轴于
交x轴于 两点,顶点为
两点,顶点为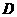 .以
.以 为直径作半圆,圆心为
为直径作半圆,圆心为 ,半圆交y轴负半轴于
,半圆交y轴负半轴于 .
.
(1)求抛物线的对称轴;
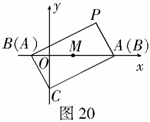
(2)将 绕圆心
绕圆心 顺时针旋转
顺时针旋转 ,得到
,得到 ,如图20.求点
,如图20.求点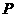 的坐标;
的坐标;
(3)有一动点 在线段
在线段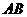 上运动,
上运动, 的周长在不断变化时是否存在最小值?若存在,求点
的周长在不断变化时是否存在最小值?若存在,求点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com