
题目列表(包括答案和解析)
6. 如图,若AB∥CD,则( )
A.∠1 = ∠4 B.∠3 = ∠5
C.∠4 = ∠5 D.∠3 = ∠4
5. 下列命题正确的是( )
A.两直线与第三条直线相交,同位角相等;
B.两直线与第三条直线相交,内错角相等;
C.两直线平行,内错角相等;
 D.两直线平行,同旁内角相等。
D.两直线平行,同旁内角相等。
4.
 如图,下列判断正确的是( )
如图,下列判断正确的是( )
A.∠1和∠5是同位角; B.∠2和∠6是同位角;
C.∠3和∠5是内错角; D.∠3和∠6是内错角.
3. 如图,AD⊥BC,DE∥AB,则∠B和∠1的关系是( )
A. 相等 B. 互补 C. 互余 D. 不能确定
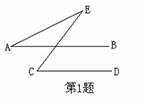


2.如图,∠1=∠2,则下列结论一定成立的是( )
A.AB∥CD B.AD∥BC C.∠B=∠D D.∠3=∠4
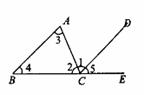
1. 如图,若AB∥CD,∠C = 60º,则∠A+∠E=( )
A.20º B.30º C.40º D.60º
(二)三角形
4. 一般三角形的性质
(1) 角与角的关系:
三个内角的和等于180°;
一个外角等于和它不相邻的两个内角之和,并且大于任何-个和它不相邻的内角。
(2) 边与边的关系:
三角形中任两边之和大于第三边,任两边之差小于第三边。
(3) 边与角的大小对应关系:
在一个三角形中,等边对等角;等角对等边。
(4) 三角形的主要线段的性质(见下表):
|
名称 |
基本性质 |
|
角平分线 |
①
三角形三条内角平分线相交于一点(内心);内心到三角形三边距离相等; ② 角平分线上任一点到角的两边距离相等。 |
|
中线 |
三角形的三条中线相交于一点。 |
|
高 |
三角形的三条高相交于一点。 |
|
边的垂直平分线 |
三角形的三边的垂直平分线相交于一点(外心); 外心到三角形三个顶点的距离相等。 |
|
中位线 |
三角形的中位线平行于第三边且等于第三边的一半。 |
5. 几种特殊三角形的特殊性质
(1) 等腰三角形的特殊性质:
①等腰三角形的两个底角相等;
②等腰三角形顶角的平分线、底边上的中线和底边上的高是同一条线段,这条线段所在的直线是等腰三角形的对称轴。
(2) 等边三角形的特殊性质:
①等边三角形每个内角都等于60°;
②等边三角形外心、内心合一。
(3) 直角三角形的特殊性质:
①直角三角形的两个锐角互为余角;
②直角三角形斜边上的中线等于斜边的一半;
③ 勾股定理:直角三角形斜边的平方等于两直角边的平方和
(其逆命题也成立);
④ 直角三角形中,30°的角所对的直角边等于斜边的一半;
⑤直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。
6. 三角形的面积
(1)
一般三角形:S △ = 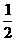 a h(
h 是a边上的高 )
a h(
h 是a边上的高 )
(2)
直角三角形:S △ = 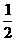 a b =
a b = 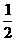 c h(a、b是直角边,c是斜边,h是斜边上的高)
c h(a、b是直角边,c是斜边,h是斜边上的高)
(3)
等边三角形: S △ = 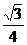 a 2( a是边长 )
a 2( a是边长 )
(4) 等底等高的三角形面积相等;等底的三角形面积的比等于它们的相应的高的比;等高的三角形的面积的比等于它们的相应的底的比。
7. 相似三角形
(1) 相似三角形的判别方法:
① 如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似;
② 如果一个三角形的两边与另一个三角形的两边对应成比例,并且夹角相等,那么这两个三角形相似;
③ 如果一个三角形的三边和另一个三角形的三边对应成比例,那么这两个三角形相似。
(2) 相似三角形的性质:
① 相似三角形对应高的比,对应中线的比,对应角平分线的比都等于相似比;
② 相似三角形的周长比等于相似比;
③ 相似三角形的面积比等于相似比的平方。
8. 全等三角形
两个能够完全重合的三角形叫全等三角形,全等三角形的对应角相等,对应边相等,其他的对应线段也相等。
判定两个三角形全等的公理或定理:
①一般三角形有SAS、ASA、AAS、SSS;
②直角三角形还有HL
(一)平行线
1. 定义:在同一平面内,不相交的两条直线叫做平行线。
2. 判定:
(1) 同位角相等,两直线平行。
(2) 内错角相等,两直线平行。
(3) 同旁内角相等,两直线平行。
(4) 垂直于同一直线的两直线平行。
3. 性质:
(1) 经过直线外一点,有且只有一条直线与这条直线平行。
(2) 如果两条直线都与第三条直线平行,那么这两条直线平行。
(3) 两直线平行,同位角相等。
(4) 两直线平行,内错角相等。
(5) 两直线平行,同旁内角互补。
8、
 解:
解: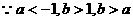
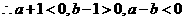
原式=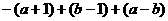
=
=
7、 =
=
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com