
题目列表(包括答案和解析)
8.解:(1)∵反比例函数 的图像经过点A(1,3),
的图像经过点A(1,3),
∴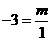 ,即m=-3.
,即m=-3.
∴反比例函数得表达式为 .
……3分
.
……3分
∵一次函数y=kx+b的图像经过A(1,-3)、C(0,-4),
∴  解得
解得
∴一次函数的表达式为y=x-4 ……3分
(2)由 消去y,得x2-4x+3=0.
消去y,得x2-4x+3=0.
即(x-1)(x-3)=0.
∴x=1或x=3.
可得y=-3或y=-1.
于是 或
或
而点A的坐标是(1,-3),
∴点B的坐标为(3,-1)。 ……2分
7. 解:(1)设药物燃烧阶段函数解析式为 ,由题意得:
,由题意得:
 ························································································································ 2分
························································································································ 2分
 .
. 此阶段函数解析式为
此阶段函数解析式为 ······································································· 3分
······································································· 3分
(2)设药物燃烧结束后的函数解析式为 ,由题意得:
,由题意得:
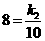 ·························································································································· 5分
·························································································································· 5分
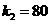 .
. 此阶段函数解析式为
此阶段函数解析式为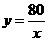 ······································································ 6分
······································································ 6分
(3)当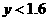 时,得
时,得 ···················································································· 7分
···················································································· 7分
 ························································································································· 8分
························································································································· 8分

 ·························································································································· 9分
·························································································································· 9分
 从消毒开始经过50分钟后学生才可回教室.···························································· 10分
从消毒开始经过50分钟后学生才可回教室.···························································· 10分
6. 解 (Ⅰ)∵点P(2,2)在反比例函数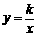 的图象上,
的图象上,
∴ .即
.即 . ···································································································· 2分
. ···································································································· 2分
∴反比例函数的解析式为 .
.
∴当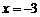 时,
时,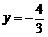 . ···························································································· 4分
. ···························································································· 4分
(Ⅱ)∵当 时,
时,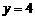 ;当
;当 时,
时,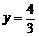 , ····················································· 6分
, ····················································· 6分
又反比例函数 在
在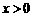 时
时 值随
值随 值的增大而减小, ············································· 7分
值的增大而减小, ············································· 7分
∴当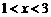 时,
时, 的取值范围为
的取值范围为 .································································ 8分
.································································ 8分
5. (1)证明:分别过点C、D作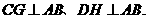
垂足为G、H,则

(2)①证明:连结MF,NE
设点M的坐标为 ,点N的坐标为
,点N的坐标为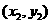 ,
,
∵点M,N在反比例函数 的图象上,
的图象上,
∴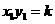 ,
,


由(1)中的结论可知:MN∥EF。
②MN∥EF。

4.  解:(1)由题意可知,
解:(1)由题意可知,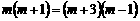 .
.
解,得 m=3. ………………………………3分
∴ A(3,4),B(6,2);
∴ k=4×3=12. ……………………………4分
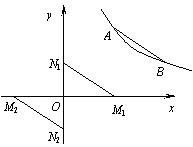
(2)存在两种情况,如图:
①当M点在x轴的正半轴上,N点在y轴的正半轴
上时,设M1点坐标为(x1,0),N1点坐标为(0,y1).
∵ 四边形AN1M1B为平行四边形,
∴ 线段N1M1可看作由线段AB向左平移3个单位,
再向下平移2个单位得到的(也可看作向下平移2个单位,再向左平移3个单位得到的).
由(1)知A点坐标为(3,4),B点坐标为(6,2),
∴ N1点坐标为(0,4-2),即N1(0,2); ………………………………5分
M1点坐标为(6-3,0),即M1(3,0). ………………………………6分
设直线M1N1的函数表达式为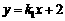 ,把x=3,y=0代入,解得
,把x=3,y=0代入,解得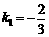 .
.
∴ 直线M1N1的函数表达式为 . ……………………………………8分
. ……………………………………8分
②当M点在x轴的负半轴上,N点在y轴的负半轴上时,设M2点坐标为(x2,0),N2点坐标为(0,y2).
∵ AB∥N1M1,AB∥M2N2,AB=N1M1,AB=M2N2,
∴ N1M1∥M2N2,N1M1=M2N2.
∴ 线段M2N2与线段N1M1关于原点O成中心对称.
∴ M2点坐标为(-3,0),N2点坐标为(0,-2). ………………………9分
设直线M2N2的函数表达式为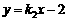 ,把x=-3,y=0代入,解得
,把x=-3,y=0代入,解得 ,
,
∴ 直线M2N2的函数表达式为 .
.
所以,直线MN的函数表达式为 或
或 . ………………11分
. ………………11分
(3)选做题:(9,2),(4,5). ………………………………………………2分
3. 解:(1) ………(每个点坐标写对各得2分)………………………4分
………(每个点坐标写对各得2分)………………………4分
 (2) ∵
(2) ∵ ∴
∴ …1分
…1分
∴ …………………1分
…………………1分
∴ …………………2分
…………………2分
(3) ① ∵
∵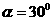
∴相应B点的坐标是
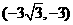 …………………………………………1分
…………………………………………1分
∴. ………………………………………………………………1分
………………………………………………………………1分
② 能 ……………………………………………………………………1分
当 时,相应
时,相应 ,
, 点的坐标分别是
点的坐标分别是 ,
,
经经验:它们都在 的图象上
的图象上
 …………………………………………………………………1分
…………………………………………………………………1分
2. 解:(1)(-4,-2);(-m,-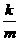 )
)
(2) ①由于双曲线是关于原点成中心对称的,所以OP=OQ,OA=OB,所以四边形APBQ一定是平行四边形
②可能是矩形,mn=k即可
不可能是正方形,因为Op不能与OA垂直。
解:(1)作BE⊥OA,
∴ΔAOB是等边三角形
∴BE=OB·sin60o= ,
,
∴B( ,2)
,2)
∵A(0,4),设AB的解析式为 ,所以
,所以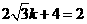 ,解得
,解得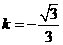 ,的以直线AB的解析式为
,的以直线AB的解析式为

(2)由旋转知,AP=AD, ∠PAD=60o,
∴ΔAPD是等边三角形,PD=PA=
1.  证明:(1)分别过点C,D,作CG⊥AB,DH⊥AB,
证明:(1)分别过点C,D,作CG⊥AB,DH⊥AB,
垂足为G,H,则∠CGA=∠DHB=90°.……1分
∴ CG∥DH.
∵ △ABC与△ABD的面积相等,
∴ CG=DH. …………………………2分
∴ 四边形CGHD为平行四边形.
∴ AB∥CD. ……………………………3分
(2)①证明:连结MF,NE. …………………4分
设点M的坐标为(x1,y1),点N的坐标为(x2,y2).
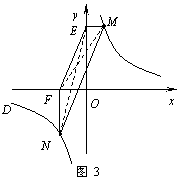 ∵ 点M,N在反比例函数
∵ 点M,N在反比例函数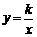 (k>0)的图象上,
(k>0)的图象上,
∴ 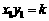 ,
,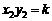 .
.
∵ ME⊥y轴,NF⊥x轴,
∴ OE=y1,OF=x2.
∴ S△EFM= , ………………5分
, ………………5分
S△EFN=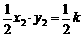 . ………………6分
. ………………6分
∴S△EFM =S△EFN. ……
由(1)中的结论可知:MN∥EF. ………8分
② MN∥EF. …………………10分
(若学生使用其他方法,只要解法正确,皆给分.
24.(1,1);
17.  18.
18. 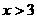 19.
19.  20.
20.  21.
21.  22. 51.2 23.
22. 51.2 23. 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com