
题目列表(包括答案和解析)
8. 解:(1)a=2,b=0.125
(2)图略
(3)设一等奖x人,二等奖y人,依题意得
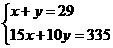
解得 所以他们共获奖金=50×9+30×20=1050元。
所以他们共获奖金=50×9+30×20=1050元。
7. 解:(1)
(2)画出直线 的图象.
的图象.
由图象得出方程的近似解为:
 .
.
6. 解:(1)线段 与
与 的位置关系是
的位置关系是 ;
;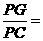
 .
.
 (2)猜想:(1)中的结论没有发生变化.
(2)猜想:(1)中的结论没有发生变化.
证明:如图,延长 交
交 于点
于点 ,连结
,连结 .
.
 是线段
是线段 的中点,
的中点, .
.
由题意可知 .
. .
.
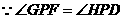 ,
, .
. ,
, .
.
 四边形
四边形 是菱形,
是菱形, ,
, .
.
由 ,且菱形
,且菱形 的对角线
的对角线 恰好与菱形
恰好与菱形 的边
的边 在同一条直线上,
在同一条直线上,
可得 .
. .
. 四边形
四边形 是菱形,
是菱形, .
.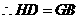 .
.
 .
.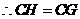 ,
, .
. .
.
即 .
. ,
, ,
, ,
, .
. .
.
 (3)
(3)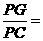
 .
.
5. 解:(1)10,30
(2)由图知: ,
,
 ,
,
 线段
线段 的解析式:
的解析式:
 ,
, ,
, 折线
折线 的解析式为:
的解析式为:
(3)由 解得
解得 ,
, 登山6.5分钟时乙追上甲.
登山6.5分钟时乙追上甲.
此时乙距 地高度为
地高度为 (米)
(米)
4. 证明:∵∠QAP=∠BAC
∴∠QAP+∠PAB=∠PAB+∠BAC
即∠QAB=∠PAC
在△ABQ和△ACP中
AQ=AP
∠QAB=∠PAC
AB=AC
3. Ⅰ.证明:∵DEFG为正方形,
∴GD=FE,∠GDB=∠FEC=90°
∵△ABC是等边三角形,∴∠B=∠C=60°
∴△BDG≌△CEF(AAS)
 Ⅱa.解法一:设正方形的边长为x,作△ABC的高AH,
Ⅱa.解法一:设正方形的边长为x,作△ABC的高AH,
求得
由△AGF∽△ABC得:
解之得: (或
(或 )
)
解法二:设正方形的边长为x,则
在Rt△BDG中,tan∠B= ,
,
∴
解之得: (或
(或 )
)
解法三:设正方形的边长为x,
则
由勾股定理得:
解之得:
Ⅱb.解: 正确
由已知可知,四边形GDEF为矩形
 ∵FE∥F’E’ ,
∵FE∥F’E’ ,
∴ ,
,
同理 ,
,
∴
又∵F’E’=F’G’,
∴FE=FG
因此,矩形GDEF为正方形
2. 观察计算
(1) ;
;
(2) .
.
探索归纳
(1)① ;②
;② ;
;
(2) .
.
①当 ,即
,即 时,
时, ,
,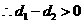 .
. ;
;
②当 ,即
,即 时,
时, ,
, .
. ;
;
③当 ,即
,即 时,
时, ,
, .
. .
.
综上可知:当 时,选方案二;
时,选方案二;
当 时,选方案一或方案二;
时,选方案一或方案二;
当 (缺
(缺 不扣分)时,选方案一.
不扣分)时,选方案一.
1. (1)证明:分别过点C、D作
垂足为G、H,则

(2)①证明:连结MF,NE
设点M的坐标为 ,点N的坐标为
,点N的坐标为 ,
,
∵点M,N在反比例函数 的图象上,
的图象上,
∴ ,
,


由(1)中的结论可知:MN∥EF。
②MN∥EF。

1.10; 2.4;
1.D 2.D 3.D 4.B 5.C 6.A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com