6、有长度分别为4 cm、5 cm、9 cm各若干根的小木棍，从中任取三根最多能组成周长不相等的等腰三角形的个数是(　 )

　 A．6　　　　 B．7　　　　　 C．8　　　　 D．9

5、四个半径为的圆如图放置，相邻两个圆交点之间的距离也为，不相邻两个圆的圆周上两点间的最短距离等于2，则的值是　　　　 ．

4、初三的灵灵从小就喜欢动手动脑，请看他的研究：

⑴以AB为直径画半圆O；⑵在半圆O上任取一点C；

⑶画∠ACB的角平分线与AB相交于点D；

⑷画CD的中垂线L与AC、BC分别相交于E、F；

⑸连结DE、DF．

如图，他发现：①∠ADE与∠BDF互余；②四边形CEDF为正方形；③四边形CEDF的面积为AE×BF．你认为其中正确的有(　　 )．

A．0个　　 B．1个　　 C．2个　　　 D．3个

3、如图，直线轴交于点A，与直线交于点B，且直线与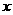轴交于点C，则的面积为　　　.

2、如图，将直角三角形ABC绕C点顺时针旋转90⁰到三角形A′B′C的位置，已知斜边AB=5，BC=3，M为A′B′的中点，则AM=__________.

1、将一个无盖正方形纸盒展开(如图①)，沿虚线剪开，用得到的5张纸片(其中4张是全等的直角三角形纸片)拼成一个正方形(如图②)，则所剪得得直角三角形较短得与较长得直角边的比是　　　 。

13、如图，Rt△AOB是一张放在平面直角坐标系中的三角形纸片，点O与原点重合，点A在x轴上，点B在y轴上，，∠BAO＝30°，将Rt△AOB折叠，使OB边落在AB边上，点O与点D重合，折痕为BE。

⑴求点E和点D的坐标；

⑵求经过O、D、A三点的二次函数解析式；

⑶设直线BE与⑵中二次函数图象的对称轴交于点F，M为OF中点，N为AF中点，在x轴上是否存在点P，使△PMN的周长最小，若存在，请求出点P的坐标和最小值；若不存在，请说明理由。

12、已知，如图，直角坐标系中的等腰梯形ABCD，AB∥CD，下底AB在x轴上，D在y轴上，M为AD的中点，过O作腰BC的垂线交BC于点E.

(1)求证：OM⊥OE；

(2)若等腰梯形中AD所在的直线的解析式为，且，求过等腰梯形ABCD的三个顶点的抛物线的解析式。

(3)若点M在梯形ABCD内沿水平方向移动到N，且使四边形MNCD为平行四边形，抛物线上是否存在一点P，使S_△PAB与四边形MNCD的面积相等，若存在，求出P点的坐标；若不存在，请说明理由。

11、如图，在Rt△AOB中，∠AOB=90°，OA=3cm，OB=4cm，以点O为坐标原点建立坐标系，设P、Q分别为AB、OB边上的动点它们同时分别从点A、O向B点匀速运动，速度均为1cm/秒，设P、Q移动时间为t(0≤t≤4)

(1)过点P做PM⊥OA于M，求证：AM：AO=PM：BO=AP：AB，并求出P点的坐标(用t表示)

(2)求△OPQ面积S(cm²)，与运动时间t(秒)之间的函数关系式，当t为何值时，S有最大值？最大是多少？

(3)当t为何值时，△OPQ为直角三角形？

(4)证明无论t为何值时，△OPQ都不可能为正三角形。若点P运动速度不变改变Q 的运动速度，使△OPQ为正三角形，求Q点运动的速度和此时t的值。

10、在某张航海图上，标明了三个观测点的坐标为O(0，0)、B(12，0)、C(12，16)，由三个观测点确定的圆形区域是海洋生物保护区，如图所示．

(1)求圆形区域的面积(取3.14)；

(2)某时刻海面上出现一渔船A，在观测点O测得A位于北偏东45°方向上，同时在观测点B测得A位于北偏东30°方向上，求观测点B到渔船A的距离(结果保留三个有效数字)；

(3)当渔船A由(2)中的位置向正西方向航行时，是否会进入海洋生物保护区？请通过计算解释．