
题目列表(包括答案和解析)
9、(1)坡度(或坡比)是坡面的 高度(h)和 长度(l)的比。
记作i,即i = ;
(2)坡角--坡面与水平面的夹角。记作α,有i= =tanα
=tanα
(3)坡度与坡角的关系:坡度越大,坡角α就越 ,坡面就越
8、图中角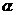 可以看作是点A的
角
可以看作是点A的
角
也可看作是点B的 角;
7、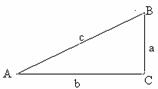 在Rt△ABC中,∠C=90゜,AB=c,BC=a,AC=b,
在Rt△ABC中,∠C=90゜,AB=c,BC=a,AC=b,
1)、三边关系(勾股定理):
2)、锐角间的关系:∠ +∠ = 90°
3)、边角间的关系:sinA = ; sinB = ;
cosA = ; cosB= ;
tanA = ; tanB = ;
 cotA = ;cotB =
cotA = ;cotB =
6、填表

5、sinA = cos(90°- ); cosA = sin( - )
tanA =cot( ); cotA =
4、tan A•cotA = ; tan B•cotB = ;
3、正弦、余弦值的大小范围: <sin A< ; <cos A<
2、锐角三角函数值,都是 实数(正、负或者0);
1、锐角∠A的三角函数(按右图Rt△ABC填空)
∠A的正弦:sinA = ,
∠A的余弦:cosA = ,
∠A的正切:tanA = ,
∠A的余切:cotA =
(三)解答题
1、略;2、3cm; 3、∵AB=BC,∴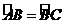 ,∴∠ADB=∠CDB,∵∠ABD=∠ACD,∴△ABD∽△DPC;
,∴∠ADB=∠CDB,∵∠ABD=∠ACD,∴△ABD∽△DPC;
4、40度;5、(-2,0),(8,0);
(0,4)、(0,-4) ;6、 ;
;
7、连结OC,证明△POC≌△POB,得∠PCO=∠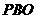 =90度,所以PD是圆O的切线;
=90度,所以PD是圆O的切线;
8、证明:(1)连结OC。
∵PD切⊙O于点C,
又∵BD⊥PD,
∴OC∥BD。
∴∠1=∠3。
又∵OC=OB,
∴∠2=∠3。
∴∠1=∠2,即BC平分∠PBD。
(2)连结AC。
∵AB是⊙O的直径,
∴∠ACB=90°。
又∵BD⊥PD,
∴∠ACB=∠CDB=90°
又∵∠1=∠2,
∴△ABC∽△CBD
∴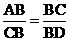 ,
,
∴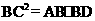
9、(1)OC∥ED;(2)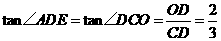
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com