
题目列表(包括答案和解析)
2.平行线与相交线:线段垂直平分线及性质;相交线中“两线四角”及“三线八角”中形成的对顶角、同位角、内错角、同旁内角等角与角之间的关系;平行线的性质及判定;平行线间的距离及平行线、垂线的画法等.
1.角:会计算角度;认识度、分、秒,会进行简单的换算;了解角平分线及其性质.
8.如图19,小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图20),量得他们的斜边长为10cm,较小锐角为 ,再将这两张三角形纸片摆成如图21的形状,但点
,再将这两张三角形纸片摆成如图21的形状,但点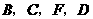 在同一条直线上,且点
在同一条直线上,且点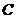 与点
与点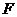 重合(在图21至图24中统一用
重合(在图21至图24中统一用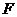 表示).
表示).
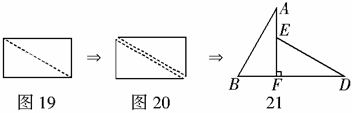
小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.
(1)将图21中的 沿BD向右平移到图22的位置,使点
沿BD向右平移到图22的位置,使点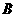 与点
与点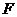 重合,请你求出平移的距离;
重合,请你求出平移的距离;
(2)将图21中的 绕点F顺时针方向旋转
绕点F顺时针方向旋转 到图23的位置,
到图23的位置,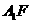 交DE于点G,请你求出线段FG的长度;
交DE于点G,请你求出线段FG的长度;
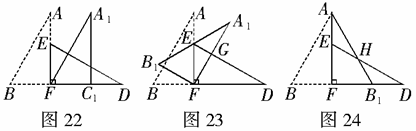
(3)将图21中的 沿直线AF翻折到图24的位置,
沿直线AF翻折到图24的位置,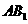 交DE于点H,请证明:
交DE于点H,请证明: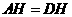 .
.
6.如图17, 中
中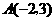 ,
,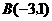 ,
,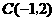 .
.
(1)将 向右平移4个单位长度,画出平移后的
向右平移4个单位长度,画出平移后的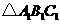 ;
;
(2)画出 关于x轴对称的
关于x轴对称的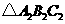 ;
;
(3)将 绕原点
绕原点 旋转
旋转 ,画出旋转后的
,画出旋转后的 ;
;
(4)在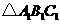 ,
, ,
,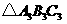 中,△______与△______成轴对称,对称轴是_________.
中,△______与△______成轴对称,对称轴是_________.
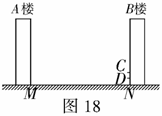 7.如图18,某居民小区内
7.如图18,某居民小区内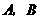 两楼之间的距离
两楼之间的距离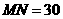 米,两楼的高都是20米,
米,两楼的高都是20米, 楼在
楼在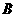 楼正南,
楼正南,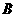 楼窗户朝南.
楼窗户朝南.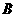 楼内一楼住户的窗台离小区地面的距离
楼内一楼住户的窗台离小区地面的距离 米,窗户高
米,窗户高 米.当正午时刻太阳光线与地面成
米.当正午时刻太阳光线与地面成 角时,
角时, 楼的影子是否影响
楼的影子是否影响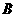 楼的一楼住户采光?若影响,挡住该住户窗户多高?若不影响,请说明理由.(参考数据:
楼的一楼住户采光?若影响,挡住该住户窗户多高?若不影响,请说明理由.(参考数据: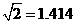 ,
,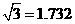 ,
,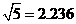 )
)
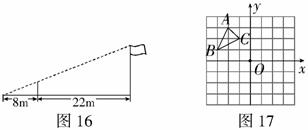
5.如图16了测量学校旗杆的高度,小东用长为3.2的竹竿做测量工具,移动竹竿,使竹杆、旗杆顶端的影子恰好落在地面的同一点,此时,竹竿与这一点相距8m,与旗杆相距22m,则旗杆的高为__________m.
4.如图15,在 中,
中,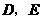 分别是
分别是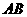 和
和 的中点,
的中点,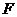 是
是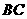 延长线上一点,
延长线上一点,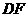 平分
平分 于点
于点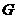 ,
,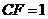 ,则
,则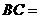 ________,
________,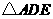 和
和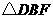 的面积之比为_________.
的面积之比为_________.
3.如图14,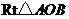 的斜边OA在y轴上,且
的斜边OA在y轴上,且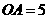 ,
,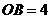 .将
.将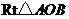 绕原点
绕原点 逆时针旋转一定的角度,使直角边
逆时针旋转一定的角度,使直角边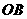 落在x轴的负半轴上得到相应的
落在x轴的负半轴上得到相应的 ,则
,则 点的坐标是________.
点的坐标是________.
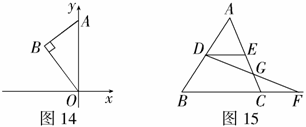
2.图形:①线段,②等边三角形,③平行四边形,④矩形,⑤梯形,⑥圆.其中既是轴对称图形又是中心对称图形的序号是_______.
5.图形与坐标:认识并能画出平面直角坐标系;在给定的直角坐标系中,会根据坐标描出点的位置、由点的位置写出它的坐标;能在方格纸上建立适当的直角坐标系,描述物体的位置;在同一直角坐标系中,感受图形变换后点的坐标的变化,灵活运用不同的方式确定物体的位置.
热点1:轴对称图形和中心对称图形的识别
例1 (2008郴州) 下列图形中,你认为既是中心对称图形又是轴对称图形的是( )

分析:把图形沿某一直线对折,若直线两旁的部分能够完全重合,则该图形为轴对称图形;若把图形绕某一点旋转 后能与自身重合,则该图形为中心对称图形,因此,可知(C)是中心对称图形,它不是轴对称图形;(B)、(D)既不是轴对称图形,也不是中心对称图形;
后能与自身重合,则该图形为中心对称图形,因此,可知(C)是中心对称图形,它不是轴对称图形;(B)、(D)既不是轴对称图形,也不是中心对称图形;
解:选(A).
点评:判断一个已知图形是不是轴对称图形或中心对称图形的关键是能否找到对称轴或对称中心,另外对于一些常见的几何图形要能对其对称性正确作出判断,而且要能掌握它的对称轴.对称中心分别是哪些直线和什么样的点,轴对称是中学数学的一个重要内容,也是中考的重要考点之一.
热点2:利用图形变换的知识求作图形、设计图案等问题
例2 (2008长沙)如图1是某设计师在方格纸中设计图案的一部分,请你帮他完成余下的工作:

(1)作出关于直线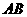 的轴对称图形;
的轴对称图形;
(2)将你画出的部分连同原图形绕点 逆时针旋转
逆时针旋转 ;
;
(3)发挥你的想象,给得到的图案适当涂上阴影,让图案变得更加美丽.
分析:本题综合考查了图形变换的几个知识点.无论作轴对称图形,还是旋转作图,画出关键点变化以后的位置,再连线,是解决这类问题的基本方法.
解:略.
点评:本题立意新颖,综合性强,将图形变换知识的考查趣味化,解题的关键是认真审题,发现规律.利用平移与旋转来设计图案,实质上也是平移与旋转的特征的应用.
热点3:图形与坐标知识,建立适当的直角坐标系描述物体的位置、图形的变换与坐标的变化、用不同的方式确定物体的位置
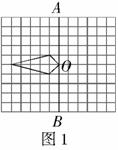
例 3 (2008岳阳)如图2,在一个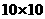 的正方形DEFG网格中有一个
的正方形DEFG网格中有一个 .
.
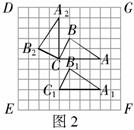
(1)在网格中画出 向下平移3个单位得到的
向下平移3个单位得到的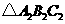 ;
;
(2)在网格中画出 绕C点逆时针方向旋转
绕C点逆时针方向旋转 得到的
得到的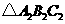 ;
;
(3)若以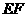 所在直线为x轴,
所在直线为x轴,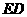 所在的直线为y轴建立直角坐标系,写出
所在的直线为y轴建立直角坐标系,写出 ,
,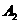 两点的坐标.
两点的坐标.
分析:在坐标平面内描出相应的点,是基本的教学目标,是画好图象的基础和前提,千万不可小视.
解:(1)、(2)见图;(3)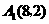 ,
,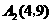 ,
,
点评:图形与坐标的考查淡化了坐标的代数性质,强调了坐标与图形的联系,形式多样,一般不难.一般以作图题题型出现较多,且与平移、旋转、对称等相结合,重点考查平面直角坐标系内点的坐标特征.
热点4:突出“双基”,灵活考查相似三角形的判定
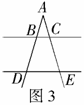 例4 (2008永州)如图3,添上条件:____________,则
例4 (2008永州)如图3,添上条件:____________,则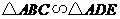 .
.
解: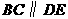 或
或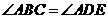 或
或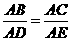 等.
等.
分析:这类考题题干简单,但是要求同学具备一定的探究能力,注意观察图形,还要对相似三角形的判定条件能够熟练掌握才能顺利答题,这类考题是基础型考题.
热点5:相似三角形与圆当中的有关知识结合,灵活运用三角形相似解题.
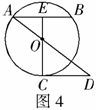 例5 (2008张家界)如图4,已知
例5 (2008张家界)如图4,已知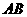 为圆
为圆 的弦(非直径),
的弦(非直径),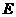 为
为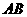 的中点,
的中点,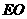 的延长线交圆于点
的延长线交圆于点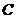 ,
, ,且交
,且交 的延长线于点
的延长线于点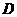 ,
, ,
,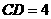 ,求圆
,求圆 的半径.
的半径.
分析:本考题先利用三角形相似求一边长,又利用直角三角形的勾股定理求半径.
解:∵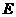 是
是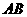 的中点,∴
的中点,∴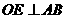 ,即
,即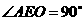 ,
,
∵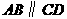 ,∴
,∴ .
.
∵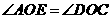 ,∴
,∴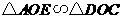 ,
,
∴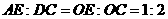 ,∴
,∴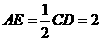 ,
,
又∵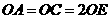 ,而
,而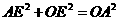 ,
,
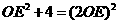 ,
,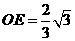 ,
,
圆 的半径
的半径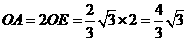 .
.
点评:转化的思想方法是数学的基本思想方法之一,圆当中求关于弦、半径等问题时,通常要转化到三角形当中来计算.
热点6:相似三角形与函数的有关知识结合,利用三角形相似相关性质解题.
例6 (2008常德)把两块全等的直角三角板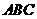 和
和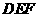 叠放在一起,使三角板
叠放在一起,使三角板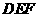 的锐角顶点
的锐角顶点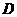 与三角板
与三角板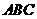 的斜边中点
的斜边中点 重合,其中
重合,其中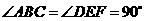 ,
,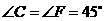 ,
,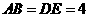 ,把三角板
,把三角板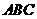 固定不动,让三角板
固定不动,让三角板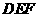 绕点
绕点 旋转,设射线
旋转,设射线 与射线
与射线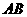 相交于点
相交于点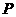 ,射线
,射线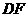 与线段
与线段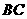 相交于点
相交于点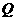 .
.
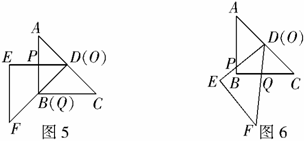
(1)如图5,当射线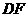 经过点
经过点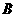 ,即点
,即点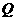 与点
与点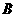 重合时,易证
重合时,易证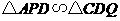 .此时,
.此时, ________.
________.
(2)将三角板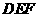 由图5所示的位置绕点
由图5所示的位置绕点 沿逆时针方向旋转至图6,设旋转角为
沿逆时针方向旋转至图6,设旋转角为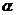 .其中
.其中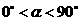 ,问
,问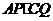 的值是否改变?说明你的理由.
的值是否改变?说明你的理由.
(3)在(2)的条件下,设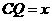 ,两块三角板重叠面积为y,求y与x的函数关系式.
,两块三角板重叠面积为y,求y与x的函数关系式.
分析:本题综合考查函数、相似三角形、动点问题,第三问通过分析不同情况下两个三角板的位置,确定函数解析式.
解:(1)8;
(2)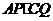 的值不会改变.
的值不会改变.
理由如下:在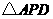 与
与 中,
中,
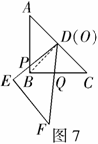
 ,
,
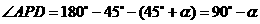 ,
,
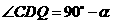 ,
,
∴ ,
,
∴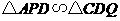 ,∴
,∴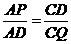 ,
,
∴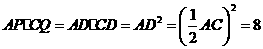 .
.
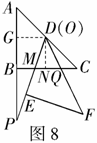
(3)情形1:当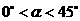 时,
时, ,即
,即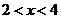 ,此时两三角板重叠部分为四边形
,此时两三角板重叠部分为四边形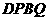 ,过
,过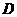 作
作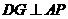 于
于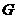 ,
,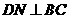 于
于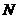 ,
,
 ∴
∴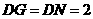 ,
,
由(2)知: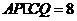 ,
,
得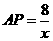 .
.
于是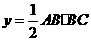
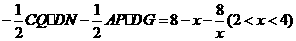 .
.
情形2:当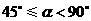 时,
时,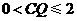 时,即
时,即 ,此时两三角板重叠部分为
,此时两三角板重叠部分为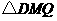 ,由于
,由于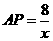 ,
,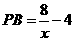 ,
,
易证: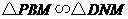 ,∴
,∴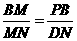
即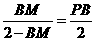 解得
解得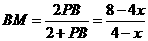 ,
,
∴ ,
,
于是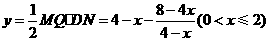 .
.
综上所述,当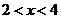 时,
时,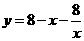 .
.
当 时,
时,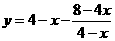 .
.
点评:这类题一般是证明相似,计算线段长、面积、猜想线段间的关系,写出函数关系式等,要想正确解答这类题型,要熟练掌握三角形相似的判定方法和性质,而且还要熟悉基本图形,能从复杂的图形中分解出基本图形,利用相似三角形的相关知识解题.
热点7:准确把握直角三角形三角函数的定义,进行简单运算.
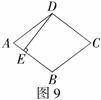 例7 (2008怀化)如图9,菱形
例7 (2008怀化)如图9,菱形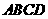 的周长为40cm,
的周长为40cm,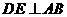 ,垂足为
,垂足为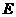 ,
,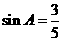 ,则下列结论正确的有( )
,则下列结论正确的有( )
①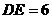 cm; ②
cm; ②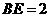 cm;
cm;
③菱形面积为 ; ④
; ④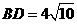 cm.
cm.
(A)1个 (B)2个 (C)3个 (D)4个
分析:在直角三角形中,在知道其中的两个元素(至少有一个是边)后,就可求出其余的元素.
解:(C).
点评:本考题在解直角三角形中的边和角的问题时,把锐角三角函数的定义与勾股定理以及其他图形的性质结合起来综合运用.
 热点8:合理利用解直角三角形,解决生活中的常见问题.
热点8:合理利用解直角三角形,解决生活中的常见问题.
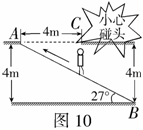
例8 (2008长沙)如图10所示,某超市在一楼至二楼之间安装有电梯,天花板与地面平行,请你根据图中数据计算回答:小敏身高1.78米,她乘电梯会有碰头危险吗?姚明身高2.29米,他乘电梯会有碰头危险吗?(可能用到的参考数值: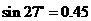 ,
,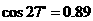 ,
,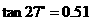 )
)
分析:本考题以姚明的身高为背景让学生体会到“生活中的身高”中的数学,解题的关键是将实际问题转化为解直角三角形问题.
解:作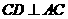 交
交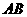 于
于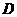 ,则
,则 ,
,
在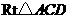 中,
中, (米).
(米).
所以小敏不会有碰头危险,姚明则会有碰头危险.
点评:考查同学们对应用问题的数学化、数学建模思想的掌握是中考的热点,要根据题意构造合适的直角三角形,从而准确迅速的解答,这也是转化思想的体现.
热点9:深刻理解三角形相似和解直角三角形,设计实际操作、开放探究结合的综合问题.
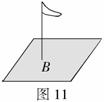 例9 某中学平整的操场上有一根旗杆(如图11),一数学兴趣小组欲测量其高度,现有测量工具(皮尺、测角仪、标杆)可供选用,请你用所学知识,帮助他们设计测量方案.
例9 某中学平整的操场上有一根旗杆(如图11),一数学兴趣小组欲测量其高度,现有测量工具(皮尺、测角仪、标杆)可供选用,请你用所学知识,帮助他们设计测量方案.
要求:(1)画出你设计的测量平面图;
(2)简述测量方法,并记录测量数据(长度用a,b,c…表示;角度用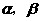 …… 表示);
…… 表示);
(3)根据你的测量的数据,计算旗杆的高度.
分析:本考题有多种方法解题,可以从三角形相似和解直角三角形中,把握性质定理来解题.
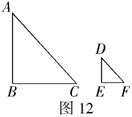 解:测量的方法有多种,如图:立标杆
解:测量的方法有多种,如图:立标杆 如图12所示,在平行太阳光AC,DF的照射下AB的影子是BC,DE的影子是EF,且
如图12所示,在平行太阳光AC,DF的照射下AB的影子是BC,DE的影子是EF,且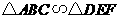 ,得到
,得到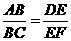 量得
量得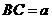 ,
,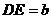 ,
, .
.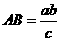 .
.
点评:设计方案题是一种创新题型,它是考查同学们运用数学知识解决实际问题能力的热点题,它对提高同学们动手操作能力和空间想象力有着重要作用.
[考题预测]
 1.已知:如图13,
1.已知:如图13, 的顶点坐标分别为
的顶点坐标分别为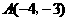 ,
,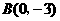 ,
,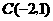 ,如将
,如将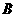 点向右平移2个单位后再向上平移4个单位到达
点向右平移2个单位后再向上平移4个单位到达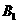 点,若设
点,若设 的面积为
的面积为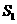 ,
,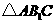 的面积为
的面积为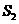 ,则
,则 的大小关系为( )
的大小关系为( )
(A)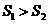 (B)
(B)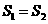
(C)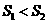 (D)不能确定
(D)不能确定
4.图形的相似:了解比例的基本性质,能通过具体实例了解黄金分割;通过具体实例认识图形的相似,探索相似图形的性质;了解两个三角形相似的概念,探索两个三角形相似的条件;了解图形的位似;利用相似解决一些实际问题;通过实例认识锐角三角函数;运用三角函数解决与直角三角形有关的简单问题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com