
题目列表(包括答案和解析)
14、130° 15、140° 16、40° 17、65° 18、36cm2
9、C 10、C 11、B 12、B 13、B
1、D 2、B 3、C 4、A 5、C 6、C 7、C 8、C
如图,已知△ABC中,AB = AC,AE = AF,D是BC的中点
求证: ∠1 = ∠2
如图,已知D是BC的中点,BE⊥AE于E,CF⊥AE于F
 求证:BE = CF
求证:BE = CF
如图,CE平分∠ACB且CE⊥BD,∠DAB =∠DBA,AC = 18,△CDB的周长是28.求BD的长.

已知:如图,点D、E在△ABC的边BC上,AD=AE,BD=EC,
求证:AB=AC

*一条河的两岸有一段是平行的,在河的这一岸每隔5m有一棵树,在河的对岸每隔50m有一根电线杆,在此岸离岸边25m处看对岸,看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且这两棵树之间还有三棵树.
根据题意,画出示意图;
求河宽.
练习答案:
如图,直线a∥b,若∠1 = 50°,
则∠2 = .

如图,AB∥CD,∠1 = 40°,
 则∠2 =
.
则∠2 =
.
如图,DE∥BC,BE平分∠ABC,
若∠ADE = 80°,则∠1 = .
 如图, l1∥l2,∠1 = 105°,∠2 =
140°,
如图, l1∥l2,∠1 = 105°,∠2 =
140°,
则∠α = .
△ABC中,BC = 12cm,BC边上的高
AD = 6cm,则△ABC的面积为 .
如果一个三角形的三边长分别为x,2,3,
那么x的取值范围是 .
在△ABC中,AB = AC,∠A = 80°,则∠B = ,∠C = .
在△ABC中,∠C = 90°,∠A = 30°,BC = 4cm,则AB = .
已知直角三角形两直角边分别为6和8,则斜边上的中线长是 .
等腰直角三角形的斜边为2,则它的面积是 .
在Rt△ABC中,其中两条边的长分别是3和4,则这个三角形的面积等于 .
已知等腰三角形的一边长为6,另一边长为10,则它的周长为 .
等腰三角形底边上的高等于腰长的一半,则它的顶角度数为 .
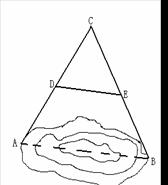 如图,A、B两点位于一个池塘的两端,冬冬想用绳子
如图,A、B两点位于一个池塘的两端,冬冬想用绳子
测量A、B两点间的距离,但绳子不够长,一位同学帮他
想了一个办法:先在地上取一个可以直接到达A、B的
点C,找到AC,BC的中点D、E,并且测得DE的长
为15m,则A、B两点间的距离为__________.
 如图,在△ABC和△DEF中,AB=DE,
如图,在△ABC和△DEF中,AB=DE,
∠B=∠E.要使△ABC≌△DEF,需要补充的
是一个条件: .
太阳光下,某建筑物在地面上的影长为36m,同时
量得高为1.2m的测杆影长为2m,那么该建筑物的高为 .
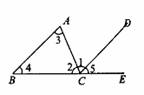
如图,若AB∥CD,∠C = 60º,则∠A+∠E=( )
A.20º B.30º C.40º D.60º
如图,∠1=∠2,则下列结论一定成立的是( )
A.AB∥CD B.AD∥BC C.∠B=∠D D.∠3=∠4
如图,AD⊥BC,DE∥AB,则∠B和∠1的关系是( )
A. 相等 B. 互补 C. 互余 D. 不能确定

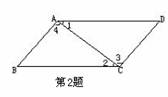

 如图,下列判断正确的是( )
如图,下列判断正确的是( )
A.∠1和∠5是同位角; B.∠2和∠6是同位角;
C.∠3和∠5是内错角; D.∠3和∠6是内错角.
下列命题正确的是( )
A.两直线与第三条直线相交,同位角相等;
B.两直线与第三条直线相交,内错角相等;
C.两直线平行,内错角相等;
 D.两直线平行,同旁内角相等.
D.两直线平行,同旁内角相等.
如图,若AB∥CD,则( )
A.∠1 = ∠4 B.∠3 = ∠5
C.∠4 = ∠5 D.∠3 = ∠4
如图, l1∥l2,则α= ( )
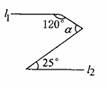 A.50°
B.80°
A.50°
B.80°
C.85° D.95°
下列长度的三条线段能组成三角形的是( )
A.3cm,4cm,8cm B.5cm,6cm,11cm
C.5cm,6cm,10cm D.3cm,8cm,12cm
等腰三角形中,一个角为50°,则这个等腰三角形的顶角的度数为( )
 A.150°
B.80°
C.50°或80°
D.70°
A.150°
B.80°
C.50°或80°
D.70°
如图,点D、E、F是线段BC的四等分点,点A在BC外,
连接AB、AD、AE、AF、AC,若AB = AC,则图中的全等三角形
共有( )对
A. 2 B. 3 C. 4 D. 5
三角形的三边分别为 a、b、c,下列哪个三角形是直角三角形?( )
A. a = 3,b = 2,c = 4 B. a = 15,b = 12,c = 9
C. a = 9,b = 8,c = 11 D. a = 7,b = 7,c = 4
 如图,△AED ∽ △ABC,AD = 4cm,AE = 3cm,
如图,△AED ∽ △ABC,AD = 4cm,AE = 3cm,
AC = 8cm,那么这两个三角形的相似比是( )
A.错误!不能通过编辑域代码创建对象。 B.错误!不能通过编辑域代码创建对象。 C.错误!不能通过编辑域代码创建对象。 D.2
下列结论中,不正确的是( )
A.有一个锐角相等的两个直角三角形相似;
B.有一个锐角相等的两个等腰三角形相似;
C.各有一个角等于120°的两个等腰三角形相似;
 D.各有一个角等于60°的两个等腰三角形相似.
D.各有一个角等于60°的两个等腰三角形相似.
(二)三角形
一般三角形的性质
角与角的关系:
三个内角的和等于180°;
一个外角等于和它不相邻的两个内角之和,并且大于任何-个和它不相邻的内角.
边与边的关系:
三角形中任两边之和大于第三边,任两边之差小于第三边.
边与角的大小对应关系:
在一个三角形中,等边对等角;等角对等边.
三角形的主要线段的性质(见下表):
|
名称 |
基本性质 |
|
角平分线 |
三角形三条内角平分线相交于一点(内心);内心到三角形三边距离相等; 角平分线上任一点到角的两边距离相等. |
|
中线 |
三角形的三条中线相交于一点. |
|
高 |
三角形的三条高相交于一点. |
|
边的垂直平分线 |
三角形的三边的垂直平分线相交于一点(外心); 外心到三角形三个顶点的距离相等. |
|
中位线 |
三角形的中位线平行于第三边且等于第三边的一半. |
几种特殊三角形的特殊性质
等腰三角形的特殊性质:
①等腰三角形的两个底角相等;
②等腰三角形顶角的平分线、底边上的中线和底边上的高是同一条线段,这条线段所在的直线是等腰三角形的对称轴.
等边三角形的特殊性质:
①等边三角形每个内角都等于60°;
②等边三角形外心、内心合一.
直角三角形的特殊性质:
①直角三角形的两个锐角互为余角;
②直角三角形斜边上的中线等于斜边的一半;
勾股定理:直角三角形斜边的平方等于两直角边的平方和
(其逆命题也成立);
直角三角形中,30°的角所对的直角边等于斜边的一半;
⑤直角三角形被斜边上的高分成的两个直角三角形和原三角形相似.
三角形的面积
一般三角形:S △ = 错误!不能通过编辑域代码创建对象。a h( h 是a边上的高 )
直角三角形:S △ = 错误!不能通过编辑域代码创建对象。a b = 错误!不能通过编辑域代码创建对象。c h(a、b是直角边,c是斜边,h是斜边上的高)
等边三角形: S △ = 错误!不能通过编辑域代码创建对象。a 2( a是边长 )
等底等高的三角形面积相等;等底的三角形面积的比等于它们的相应的高的比;等高的三角形的面积的比等于它们的相应的底的比.
相似三角形
相似三角形的判别方法:
如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似;
如果一个三角形的两边与另一个三角形的两边对应成比例,并且夹角相等,那么这两个三角形相似;
如果一个三角形的三边和另一个三角形的三边对应成比例,那么这两个三角形相似.
相似三角形的性质:
相似三角形对应高的比,对应中线的比,对应角平分线的比都等于相似比;
相似三角形的周长比等于相似比;
相似三角形的面积比等于相似比的平方.
全等三角形
两个能够完全重合的三角形叫全等三角形,全等三角形的对应角相等,对应边相等,其他的对应线段也相等.
判定两个三角形全等的公理或定理:
①一般三角形有SAS、ASA、AAS、SSS;
②直角三角形还有HL
(一)平行线
定义:在同一平面内,不相交的两条直线叫做平行线.
判定:
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角相等,两直线平行.
垂直于同一直线的两直线平行.
性质:
经过直线外一点,有且只有一条直线与这条直线平行.
如果两条直线都与第三条直线平行,那么这两条直线平行.
两直线平行,同位角相等.
两直线平行,内错角相等.
两直线平行,同旁内角互补.
8、 
 解:
解:

原式=
=
=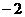
本资料由《七彩教育网》 提供!
7、  =
=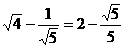
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com