
题目列表(包括答案和解析)
7、蔬菜基地种植某种蔬菜,由市场行情分析知,1月份至6月份这种蔬菜的上市时间x(月份)与市场售价P(元/千克)的关系如下表:
|
上市时间x(月份) |
1 |
2 |
3 |
4 |
5 |
6 |
|
市场售价P(元/千克) |
10.5 |
9 |
7.5 |
6 |
4.5 |
3 |
这种蔬菜每千克的种植y(元/千克)与上市时间(月份)满足
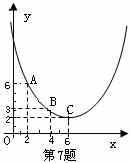
一个函数关系式,这个函数的图象是抛物线的一段(如图)。
(1) 写出上表中表示的市场售价P(元/千克)关于上市时间x(月份)的函数关系式;
(2) 若抛物线过点A、B、C三点,写出抛物线对应的函数关系式;
(3)
 由以上信息分析,哪个月上市出售这种蔬菜每千克的收益最大?最大值是多少?(收益=市场售价-种植成本)
由以上信息分析,哪个月上市出售这种蔬菜每千克的收益最大?最大值是多少?(收益=市场售价-种植成本)
6、 已知抛物线 ,(1)当
,(1)当 时,求此抛物线的顶点坐标和对称轴;(2)若代数式
时,求此抛物线的顶点坐标和对称轴;(2)若代数式 的值为正整数,求x的值;(2)若
的值为正整数,求x的值;(2)若 时,抛物线
时,抛物线 与x轴的正半轴相交于点M(m,0);当
与x轴的正半轴相交于点M(m,0);当 时,抛物线
时,抛物线 与x轴的正半轴相交于点N(n,0);若点M在点N的左边,试比较
与x轴的正半轴相交于点N(n,0);若点M在点N的左边,试比较 与
与 的大小。
的大小。
5、 已知四边形ABCD是矩形,BC>AB,直线MN分别与AB、BC交于E、F两点,P为对角线AC上一动点(P不与A、C重合)。
(1) 当点E、F分别为AB、BC的中点时,如图①所示,问P点在AC上运动时,点P、E、F能否构成直角三角形?若能,共有几个,请在图中画出所有满足条件的三角形;
(2) 若AB=3,BC=4,P为AC的中点,当直线MN在移动时,始终保持MN∥AC,如图②所示,求△PEF的面积与FC的长x之间的函数关系式。

4、 如图,在
如图,在 ABCD中,AB=4,BC=3,∠BAD=120°,E为BC上一动点(不与B重合),作EF⊥AB于F,FE、DC的延长线交于点G,设BE=x,△DEF的面积为S。(1)求证:△BEF∽△CEG;(2)求出S与x之间的函数关系式,并写出自变量x的取值范围;(3)当E运动到何处时,S有最大值,最大值是多少?
ABCD中,AB=4,BC=3,∠BAD=120°,E为BC上一动点(不与B重合),作EF⊥AB于F,FE、DC的延长线交于点G,设BE=x,△DEF的面积为S。(1)求证:△BEF∽△CEG;(2)求出S与x之间的函数关系式,并写出自变量x的取值范围;(3)当E运动到何处时,S有最大值,最大值是多少?
3、如图,在正方形ABCD中,AB=2,E是AD边上一点(点E与点A、D不重合),BE的垂直平分线交AB于M,交DC于N。
(1) 设AE=x,四边形ADNM的面积为S,写出S关于x的函数关系式;
(2) 当AE为何值时,四边形ADNM的面积最大?最大值是多少?

2、如图,对称轴为直线x= 的抛物线经过点A(6,0),和B(0,4)。(1)求抛物线的解析式及顶点坐标;
的抛物线经过点A(6,0),和B(0,4)。(1)求抛物线的解析式及顶点坐标;
 (2)设点E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形,求
(2)设点E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形,求 OEAF的面积S与x之间的函数关系式,并写出自变量x的取值范围。①当
OEAF的面积S与x之间的函数关系式,并写出自变量x的取值范围。①当 OEAF的面积为24时,请判断
OEAF的面积为24时,请判断 OEAF是否为菱形?
OEAF是否为菱形?
②是否存在点E,使 OEAF为正方形?若存在,求出点E的坐标;
OEAF为正方形?若存在,求出点E的坐标;
若不存在,请说明理由。
1、 如图,在Rt△ABC中,∠C=90°,AC=12,BC=16.动点P从点A出发沿AC方向向点C以每秒3个单位长的速度运动,动点Q从点C出发沿CB边向点B以每秒4个单位长的速度运动,P、Q分别从点A、C同时出发,当其中一点到达端点时,另一点随之停止运动,设运动时间为t(秒),△PQD与△PQC关于PQ对称。(1)设四边形PCQD的面积为y,求y与t的函数关系式;(2)t为何值时,四边形PQBA是梯形?(3)是否存在时刻t,使得PD∥AB?若存在,求出t的值;若不存在,请说明理由;(4)通过观察、画图或折纸等方法,猜想是否存在时刻t使得PD⊥AB?若存在,请你估计t的值在括号中的哪个时间段内(0≤t≤1,1<t≤2,2<t≤3,3<t≤4)?若不存在,请简要说明理由。

7.如下图,一个点从数轴上的原点开始,先向右移动了3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2,

已知点A、B是数轴上的点,完成下列各题:
(1)如果点A表示数-3,将点A向右移动7个单位长度,那么终点B表示的数是_________,A、B两点间的距离是________。
(2)如果点A表示数是3,将点A向左移动7个单位长度,再向右移动5个单位长度,那么终点B表示的数是_______,A、B两点间的距离是________。一般地,如果点A表示数为a,将点A向右移动b个单位长度,再向左移动c个单位长度,那么请你猜想终点B表示的数是________,A、B两点间的距离是_________。
6. 如图,我们在数轴上以单位线段为边做一个正方形,然后以
如图,我们在数轴上以单位线段为边做一个正方形,然后以 为圆心,正方形的对角线长为半径画弧交
为圆心,正方形的对角线长为半径画弧交 轴上于一点
轴上于一点 ,则
,则 的长就是
的长就是 个单位.动手试一试,你能用类似的方法在数轴上找出表示
个单位.动手试一试,你能用类似的方法在数轴上找出表示 ,
, 的点吗?矩形对角线的长的平方等于矩形长的平方与宽的平方的和.(提示:
的点吗?矩形对角线的长的平方等于矩形长的平方与宽的平方的和.(提示: ,
, )
)
5. 一个等边圆柱(底面直径与高相等的圆柱称为等边圆柱)的体积为16 cm3,求其表面积.
cm3,求其表面积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com