
题目列表(包括答案和解析)
3.不等式组 的解集是( )
的解集是( )
(A) (B)
(B)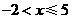
(C) (D)无解
(D)无解
2.分式方程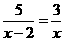 的解为
的解为 ____________.
____________.
1.方程组 的解是____________.
的解是____________.
6.如图17,已知抛物线 与x轴的一个交点
与x轴的一个交点 .
.

(1)你一定能分别求出这条抛物线与x轴的另一个交点B及与y轴的交点C的坐标,试试看;
(2)设抛物线的顶点为D,请在图中画出抛物线的草图.若点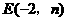 在直线BC上,试判断E点是否在经过D点的反比例函数的图象上,把你的判断过程写出来;
在直线BC上,试判断E点是否在经过D点的反比例函数的图象上,把你的判断过程写出来;
(3)请设法求出tan∠DAC的值.
本资料由《七彩教育网》 提供!
5.如图15,矩形ABCD中, ,
, ,将矩形ABCD沿对角线AC平移,平移后的矩形为EFGH(A、E、C、G始终在同一条直线上),当点E与C重合时停止移动.平移中EF与BC交于点N,GH与BC的延长线交于点M,EH与DC交于点P,FG与DC的延长线交于点Q.设S表示矩形PCMH的面积,
,将矩形ABCD沿对角线AC平移,平移后的矩形为EFGH(A、E、C、G始终在同一条直线上),当点E与C重合时停止移动.平移中EF与BC交于点N,GH与BC的延长线交于点M,EH与DC交于点P,FG与DC的延长线交于点Q.设S表示矩形PCMH的面积, 表示矩形NFQC的面积.
表示矩形NFQC的面积.
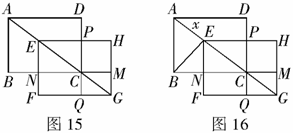
(1)  与
与 相等吗?请说明理由.
相等吗?请说明理由.
(2)设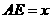 ,写出S和x之间的函数关系式,并求出x取何值时S有最大值,最大值是多少?
,写出S和x之间的函数关系式,并求出x取何值时S有最大值,最大值是多少?
(3)如图16,连结BE,当AE为何值时, 是等腰三角形.
是等腰三角形.
4.在社会主义新农村建设中,李叔叔承包了家乡的50亩荒山.经过市场调查,预测水果上市后A种水果每年每亩可获利0.3万元,B种水果每年每亩可获利0.2万元,李叔叔决定在承包的山上种植A、B两种水果.他了解到需要一次性投入的成本为:A种水果每亩1万元,B种水果每亩0.9万元.设种植A种水果x亩,投入成本总共y万元.
(1)求y与x之间的函数关系式;
(2)若李叔叔在开发时投入的资金不超过47万元,为使总利润每年不少于11.8万元,应如何安排种植面积(亩数x取整数)?请写出获利最大的种植方案.
3.已知正比例函数 经过点
经过点 ,如图14所示.
,如图14所示.
(1)求这个正比例函数的解析式;
(2)将这个正比例函数的图象向右平移4个单位,写出在这个平移下,点 、原点
、原点 的平移后所得的
的平移后所得的 的坐标,并求出平移后的直线的解析式.
的坐标,并求出平移后的直线的解析式.
2. 如图13,一次函数 与反比例函数
与反比例函数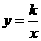 的图象相交于
的图象相交于 两点,若已知一个交点为
两点,若已知一个交点为 ,则另一个交点B的坐标为( )
,则另一个交点B的坐标为( )
(A) (B)
(B)
(C) (D)
(D)
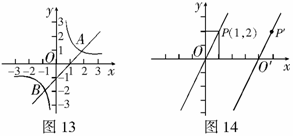
12.如图25(1)、25(2)、25(3)中,点E、D分别是正 、正四边形ABCM、正五边形ABCMN中以C点为顶点的相邻两边上的点,且BE = CD,DB交AE于P点.
、正四边形ABCM、正五边形ABCMN中以C点为顶点的相邻两边上的点,且BE = CD,DB交AE于P点.
(1)图25(1)中,∠APD的度数为________;
(2)图25(2)中,∠APD的度数为________,图25(3)中,∠APD的度数为________;
(3)根据前面探索,你能否将本题推广到一般的正n边形情况.若能,写出推广问题和结论;若不能,请说明理由.
本资料由《七彩教育网》 提供!
11.如图24,已知正方形ABCD中,E为BC上一点,将正方形折叠起来,使点A和点E重合,折痕为MN,若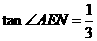 ,
, .
.
(1)求 的面积.
的面积.
(2)求 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com