23、解：

在△AEF中，∠EAF=∠β-∠α=60⁰-30⁰=30⁰

∴∠EAF=∠α，进而AF=EF=CD=50m.

在△AFG中，∵sinβ=

∴AG=AF×sin60⁰

=50×=25

≈43.30( m )

AB=AG+BG=AG+CE=43.30+1.52=44.82(m)

答：建筑物AB的高度约为44.82米。

22、证明：

连结OC

∵CD与⊙O相切于点C

∴OC⊥CD

∵OA=OC，∠OAC=∠OCA

又　　　 ∠OAC=∠DAC

∴∠OCA=∠DAC

∴AD∥OC

∴AD⊥CD

解：　 连结BC

　　 ∵AB是直径

　　 ∴∠ACB=∠ADC=90⁰，

又 ∠BAC=∠DAC

　　 ∴△ABC-△CAD

　　 ∴

　　 ∴AB=

21、解：

过点E作镜面的法线EF，

由光学原理得∠CEF=∠AEF

∵∠DEC=90⁰-∠CEF

∠BEA=90⁰-∠AEF

∴∠DEC=∠BEA

又∠CDE=∠ABE=90⁰

∴△CDE-△ABE

∴

即

解得AB=12(M)

答：旗杆AB高为12米。

20、解：

(Ⅰ)设此抛物线的解析式为y=ax²+bx+c

分别将A(-2，0)、B(1，0)、C(2，8)三点的坐标代入

得：

解得，

所求抛物线解析式为y=2x²+2x-4

(Ⅱ)将函数y=2x²+2x-4配方，

得，

∴抛物线的顶点坐标为(

19、解：

由勾股定理得，BC=

∵tanB=

∴∠B=60⁰

∴∠A=90⁰-∠B=30⁰

26、如图，四边形ABCD中，AD＝CD，∠DAB＝∠ACB＝90°，过点D作DE⊥AC，垂足为F，DE与AB相交于点E．

(1)求证：AB·AF＝CB·CD；

(2)已知AB＝15 cm，BC＝9 cm，P是线段DE上的动点．设DP＝x cm，梯形BCDP的面积为y cm²．

①求y关于x的函数关系式。

②y是否存在最大值？若有求出这个最大值，若不存在请说明理由。

塘沽区2009年初中学业考查数学模拟试卷评分细则

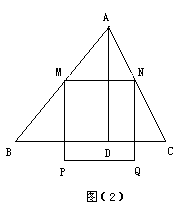
25、如图在锐角△ABC中，BC=6，S_△ABC=12两动点M、N分别在AB、AC上滑动，且MN∥BC，以MN为边长向下作正方形MPQN，设MN=x,正方形MPQN与△ABC公共部分的面积为y

(1)求出△ABC的边BC上的高。

(2)如图(1)，当正方形MPQN的边P恰好落在BC边上时，求x的值。

(3)如图(2)，当PQ落△ABC外部时，求出y与x的函数关系式。

24.某产品每件成本30元，试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表：

　 若日销售量y(件)与销售价x(元)满足一次函数y=kx+b．

　 (1)求出这个一次函数关系式；

(2)设每日的销售利润为w(元)，售价为x(元)，求出w与x的函数关系式。

(3)每件产品的销售价应定为多少元时销售利润最大?此时销售利润是多少元?

23、下表是育英中学数学课外小组测量建筑物AB的高度实验报告的部分内容

测量图形 　 　 　 测量数据
测量值	仰角∠α	仰角∠β	CD长
第一次	30023′	59037′	50.96m
第二次	29048′	60019′	49.26m
第三次	29049′	60004′	49.78m
平均值	300	600	50m

(1)完成上表中的平均值数据，将结果填在表格中

(2)若测量仪器高度EC=FD=1.52m，根据表格提供的数据计算建筑物AB的高度。

(取1.732，结果精确到0.01米)

22、如图，已知AB是⊙O的直径，直线CD与⊙O相切于点C，AC平分∠DAB。

(1)求证：AD⊥CD

(2)若AD=3，AC=，求AB的长。