
题目列表(包括答案和解析)
3]如图,矩形纸片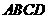 中,
中, ,将纸片折叠,使顶点
,将纸片折叠,使顶点 落在边
落在边 的
的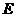 点上,折痕的一端
点上,折痕的一端 点在边
点在边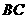 上,
上, .
.
(1)求 的面积;
的面积;
(2)求出折痕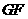 的长.
的长.


2]在平面直角坐标系内,已知点A(2,1),O为坐标原点.请你在坐标轴上确定点P,使得ΔAOP成为等腰三角形.在给出的坐标系中把所有这样的点P都找出来,画上实心点,并在旁边标上P1,P2,……,Pk,(有k个就标到PK为止,不必写出画法)
解:以A为圆心,OA为半径作圆交坐标轴得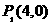 和
和 ;
;
以O为圆心,OA为半径作圆交坐标轴得 ,
, ,
, 和
和 ;作OA的垂直平分线交坐标轴得
;作OA的垂直平分线交坐标轴得 和
和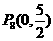 。
。


点拨:应分三种情况:①OA=OP时;②OP=P时;③OA=PA时,再找出这三种情况中所有符合条件的P点.
1]如图,在矩形ABCD中,AB=3,BC=2,点A的坐标为(1,0),以CD为直径,在矩形ABCD内作半圆,点M为圆心.设过A、B两点抛物线的解析式为y=ax2+bx+c,顶点为点N.
(1)求过A、C两点直线的解析式;
(2)当点N在半圆M内时,求a的取值范围;
 (3)过点A作⊙M的切线交BC于点F,E为切点,当以点A、F,B为顶点的三角形与以C、N、M为顶点的三角形相似时,求点N的坐标.
(3)过点A作⊙M的切线交BC于点F,E为切点,当以点A、F,B为顶点的三角形与以C、N、M为顶点的三角形相似时,求点N的坐标.
解:(1)过点A、c直线的解析式为y=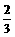 x-
x-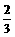
(2)抛物线y=ax2-5x+4a.
∴顶点N的坐标为(-,-a).
由抛物线、半圆的轴对称可知,抛物线的顶点在过点M且与CD垂直的直线上,
又点N在半圆内,<-a <2,解这个不等式,得-<a<-.
(3)设EF=x,则CF=x,BF=2-x
在Rt△ABF中,由勾股定理得x= ,BF=
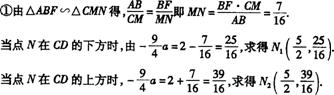

11.如图9,直线 ,连结
,连结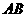 ,直线
,直线 及线段
及线段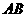 把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点
把平面分成①、②、③、④四个部分,规定:线上各点不属于任何部分.当动点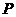 落在某个部分时,连结
落在某个部分时,连结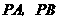 ,构成
,构成 ,
, ,
, 三个角.(提示:有公共端点的两条重合的射线所组成的角是
三个角.(提示:有公共端点的两条重合的射线所组成的角是 角.)
角.)
(1)当动点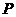 落在第①部分时,求证:
落在第①部分时,求证: ;
;
(2)当动点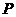 落在第②部分时,
落在第②部分时, 是否成立(直接回答成立或不成立)?
是否成立(直接回答成立或不成立)?
 (3)当动点
(3)当动点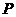 在第③部分时,全面探究
在第③部分时,全面探究 ,
, ,
, 之间的关系,并写出动点
之间的关系,并写出动点 的具体位置和相应的结论.选择其中一种结论加以证明.
的具体位置和相应的结论.选择其中一种结论加以证明.
本资料由《七彩教育网》 提供!
10.已知抛物线 与
与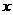 轴的交点为A、B(B在A右边),与
轴的交点为A、B(B在A右边),与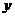 轴的交点为C.
轴的交点为C.
(1)写出 时与抛物线有关的三个正确结论;
时与抛物线有关的三个正确结论;
(2)当点B在原点的右边,点C在原点的下方时,是否存在△BOC为等腰三角形的情形?若存在,求出 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
 (3)请你提出一个对任意的
(3)请你提出一个对任意的 值都能成立的正确命题(说明:根据提出问题的水平层次,得分有差异).
值都能成立的正确命题(说明:根据提出问题的水平层次,得分有差异).
9.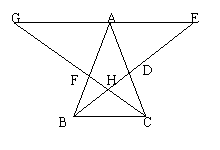 如图,△ABC中,AB=AC,过点A作GE∥BC,角平分线BD、CF相交于点H,它们的延长线分别交GE于点E、G.试在图中找出3对全等三角形,并对其中一对全等三角形给出证明.
如图,△ABC中,AB=AC,过点A作GE∥BC,角平分线BD、CF相交于点H,它们的延长线分别交GE于点E、G.试在图中找出3对全等三角形,并对其中一对全等三角形给出证明.
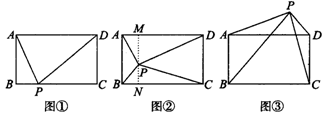
8.已知矩形ABCD和点P,当点P在边BC上任一位置(如图①所示)时,易证得结论:PA2+PC2=PB2+PD2,请你探究:当P点分别在图②、图③中的位置时,PA2、PB2、PC2和PD2又有怎样的数量关系?请你写出对上述两种情况的探究结论,并利用图②证明你的结论.
答:对图②的探究结论为__________.
对图③的探究结论为_________.
7.如图,◎Ol与◎O2相交于点A、B,顺次连结0l、A、02、B四点,得四边形01A02B.
(1)根据我们学习矩形、菱形、正方形性质时所获得的经验,探求图中的四边形有哪
些性质?(用文字语言写出4条性质)
 性质1.________________________________;
性质1.________________________________;
性质2.________________________________;
性质3.________________________________;
性质4.________________________________.
(2)设◎O1的半径为尺,◎O2的半径为r(R>r),0l,02的距离为d.当d变化时,四边形01A02B的形状也会发生变化.要使四边形01A02B是凸四边形(把四边形的任一边向两方延长,其他各边都在延长所得直线同一旁的四边形).则d的取值范围是____________________________。
6. 如图,在△ABC中,AB=AC,AD⊥BC,D为垂足.由以上两个条件可得________.(写出一个结论)
如图,在△ABC中,AB=AC,AD⊥BC,D为垂足.由以上两个条件可得________.(写出一个结论)
解:∠1=∠2或BD=DC或△ABD≌△ACD等.
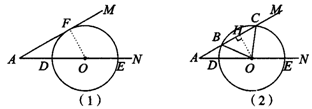
5.已知:∠MAN=30°,O为边AN上一点,以O为圆心,2为半径作⊙O,交AN于D,E两点,设AD=x.
(1)如图(1)当x取何值时,⊙O与AM相切;
(2)如图(2)当x为何值时,⊙O与AM相交于B,C两点,且∠BOC=90°.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com