
题目列表(包括答案和解析)
26、如图,已知二次函数 的图像经过点A和点B.
的图像经过点A和点B.
(1)求该二次函数的表达式;
(2)写出该抛物线的对称轴及顶点坐标;
 (3)点P(m,m)与点Q均在该函数图像上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q 到x轴的距离.
(3)点P(m,m)与点Q均在该函数图像上(其中m>0),且这两点关于抛物线的对称轴对称,求m的值及点Q 到x轴的距离.
[命题意图]考察二次函数的有关知识。
[参考答案]解:(1)将x=-1,y=-1;x=3,y=-9分别代入 得
得
 解得
解得  ……………3分
……………3分
∴二次函数的表达式为 . ………………………4分
. ………………………4分
(2)对称轴为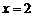 ;顶点坐标为(2,-10). …………6分
;顶点坐标为(2,-10). …………6分
(3)将(m,m)代入 ,得
,得 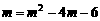 ,
,
解得 .∵m>0,∴
.∵m>0,∴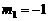 不合题意,舍去.
不合题意,舍去.
∴ m=6.………………………………10分
∵点P与点Q关于对称轴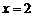 对称,
对称,
∴点Q到x轴的距离为6. …………………12分
[试题来源]资料
25、甲、乙两超市(大型商场)同时开业,为了吸引顾客,都举行有奖酬宾活动:凡购物满100元,均可得到一次摸奖的机会.在一个纸盒里装有2个红球和2个白球,除颜色外其它都相同,摸奖者一次从中摸出两个球,根据球的颜色决定送礼金券(在他们超市使用时,与人民币等值)的多少(如下表).
甲超市:
|
球 |
两红 |
一红一白 |
两白 |
|
礼金券(元) |
5 |
10 |
5 |
乙超市:
|
球 |
两红 |
一红一白 |
两白 |
|
礼金券(元) |
10 |
5 |
10 |
(1)用树状图表示得到一次摸奖机会时摸出彩球的所有情况;
(2)如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由.
[命题意图]考察概率的有关知识。
[参考答案]解:(1)树状图为:

 ……………4分
……………4分
(2)方法1:
∵ 去甲超市购物摸一次奖获10元礼金券的概率是 (甲)
(甲) , ……7分
, ……7分
去乙超市购物摸一次奖获10元礼金券的概率是 (乙)
(乙) , ………9分
, ………9分
∴ 我选择去甲超市购物. …………………………………………10分
方法2:
∵ 两红的概率P=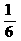 ,两白的概率P=
,两白的概率P=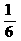 ,一红一白的概率P=
,一红一白的概率P= =
= ,…6分
,…6分
∴ 在甲商场获礼金券的平均收益是: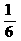 ×5+
×5+ ×10+
×10+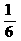 ×5=
×5=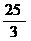 ;……8分
;……8分
在乙商场获礼金券的平均收益是: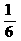 ×10+
×10+ ×5+
×5+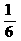 ×10=
×10= .
.
∴ 我选择到甲商场购物. ……………………………………………………10分
说明:树状图表示为如下形式且按此求解第(2)问的,也正确.

[试题来源]资料
(第26题12分)
23、.如图,在梯形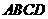 中,
中, ,对角线
,对角线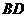 平分
平分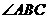 ,
, 的平分线
的平分线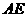 交
交 于
于 分别是
分别是 的中点.
的中点.
(1)求证: ;
;
(2)当 与
与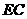 满足怎样的数量关系时,
满足怎样的数量关系时,  ?并说明理由.
?并说明理由.
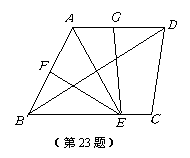
[命题意图]考察图形有关的内容。
[参考答案](1)证明:∵


又∵


又 ,
,
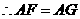 ……………3分
……………3分
又 ,
,
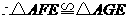
 ……………………4分
……………………4分
(2)当 时,
时,



又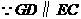
 四边形
四边形 是平行四边形
是平行四边形
 …………………………………8分
…………………………………8分
[试题来源]资料
(第22题8分)
22、如图, 是⊙
是⊙ 的直径,点
的直径,点 是半径
是半径 的中点,点
的中点,点 在线段
在线段 上运动(不与点
上运动(不与点 重合)。点
重合)。点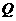 在上半圆上运动,且总保持
在上半圆上运动,且总保持 ,过点
,过点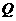 作⊙
作⊙ 的切线交
的切线交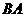 的延长线于点
的延长线于点 。
。
(1)当 时,判断
时,判断 是
三角形;
是
三角形;
(2)当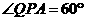 时,请你对
时,请你对 的形状做出猜想,并给予证明;
的形状做出猜想,并给予证明;
(3)由(1)、(2)得出的结论,进一步猜想,当点 在线段
在线段 上运动到任何位置时,
上运动到任何位置时, 一定是
三角形。
一定是
三角形。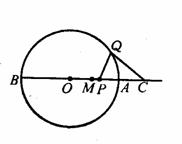
[命题意图]考察圆的有关知识。
[参考答案]解(1)等腰直角三角形
(2)当 J 等边三角形。
J 等边三角形。
证明;连结 是⊙
是⊙ 的切线
的切线



又  是等边三角形。
是等边三角形。
(3)等腰三角形。
[试题来源]资料
(第23题8分)
21、某航运公司年初用120万元购进一艘运输船,在投入运输后,每一年的总收入为72万元,需要支出的各种费用为40万元。
(1) 问:该船运输几年后开始盈利(盈利即指总收入减去购船费及所有支出费用之差为正值?)
(2) 若该船运输满15年要报废,报废时旧船卖出可收回20万元,求这15年平均盈利额(精确0.1万元)。
[命题意图]考察不等式的应用
[参考答案](1)设该船厂运输X年后开始盈利,72X-(120+40X)﹥0,X﹥ ,因而该船运输4年后开始盈利。
,因而该船运输4年后开始盈利。
(2)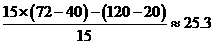 (万元)。
(万元)。
[试题来源]资料
20.先化简,再求值.  其中
其中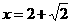 .
.
[命题意图]考察分式的通分、化简、分解因式等知识。
[参考答案]解:原式= ………………2分
………………2分
= …………………………3分
…………………………3分
= …………………………5分
…………………………5分
当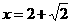 时,原式=
时,原式= ………………………………6分
………………………………6分
[试题来源]资料
(第21题6分)
(第19题6分,第20题6分)
19. 计算:
[命题意图]考察三角函数的有关知识。
[参考答案]
解:原式= ………4分
………4分
= ……………………6分
……………………6分
[试题来源]资料
13、 如图,在直线m上摆放着三个正三角形:△ABC、△HFG、△DCE,已知BC=CE,F、G分别是BC、CE的中点,FM∥AC,GN∥DC.设图中三个平行四边形的面积依次是S1,S2,S3,若S1+S3=10,则S2=
如图,在直线m上摆放着三个正三角形:△ABC、△HFG、△DCE,已知BC=CE,F、G分别是BC、CE的中点,FM∥AC,GN∥DC.设图中三个平行四边形的面积依次是S1,S2,S3,若S1+S3=10,则S2=
[命题意图]考察图形的综合应用能力。
[参考答案]4
[试题来源]资料
12.函数y= 自变量的取值范围是 .
自变量的取值范围是 .
[命题意图]考察使得分式和根号有意义的知识。
[参考答案]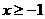 且
且
[试题来源]资料
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com