12、现有一张长和宽之比为2：1的长方形纸片．将它折两次(第一次折后也可以打开铺平再折第二次)．使得折痕将纸片分为面积相等且不重叠的四个部分(称为一个操作)，如图甲(虚线表示折痕)．

除图甲外，请你再给出三个不同的操作，分别将折痕画在图①至图③中(规定：一个操作得到的四个图形，和另一个操作得到的四个图形，如果能够“配对”得到四组全等的图形，那么就认为是相同的操作．如图乙和图甲是相同的操作)．

[试题来源]2006年浙江省中考题

[参考答案]

[命题意图]本题首先引发了学生提出方案的积极性，又关注了学生提出问题的深度和广度。学生会从不同角度展开想象的翅膀，按照自己的设计完成后的赏析中还有可能进行反思，从反思中获得解决问题的经验。

11、请你先化简，再选取一个使原式有意义，而你又喜爱的数代人求值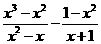

[试题来源]自编

[参考答案]略

[命题意图]初看此题很一般，其实不然。第一步化简，考察了学生基本的运算能力，使学生体会数学式子的简单美。第二步，则充分体现了“以人为本”的思想，可以培养学生的主动积极参与数学活动，获得成功体验，建立自信心的良好习惯。

10、如图8，，用灰白两色正方形瓷砖铺设地面，第n个图案中白色瓷砖数为___________．

[试题来源]2006河北中考题

[参考答案]第1个图案有白色瓷砖5(即2+3´1)块；第2个图案有白色瓷砖8(即2+3´2)块；第3个图案有白色瓷砖11(即2+3´3)块. 由此可得，第n个图案有白色瓷砖(2+3n)块. 填． 3n+2

[命题意图]根据图形提供的信息探索规律，是近几年较流行的一种探索规律型问题.解决这类问题。本题可考察学生能否由若干特例，去观察、探索、发现并归纳出一般性的结论。有利于培养学生“从问题情境出发、建立模型、寻求结论” 的意识，从而形成一定的实践能力。

9、小明在超市帮妈妈买回一袋纸杯，他把纸杯整齐地叠放

在一起，如图7请你根据图中的信息，若小明把100个纸杯

整齐叠放在一起时，它的高度约是 　　　　　　　

[试题来源]09河北中考调研卷

[参考答案]106

[命题意图]考察学生运用方程或方程组知识解决日常生活问题的能力。考题贴近生活实际，富有生活气息。当然学生也可运用算术方法解答。

8、如图5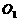，，，，为四个等圆的圆心，A，B，C，D为切点，请你在图中画出一条直线，将这四个圆分成面积相等的两部分，并说明这条直线经过的两个点是　　　　　　 ；如图6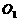，，，，，为五个等圆的圆心，A，B，C，D，E为切点，请你在图中画出一条直线，将这五个圆分成面积相等的两部分，并说明这条直线经过的两个点是　　　　　　 ．

[试题来源]天津08中考题

[参考答案]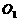，，如图①　 (提示：答案不惟一，过与交点O的任意直线都能将四个圆分成面积相等的两部分)；

，，如图②　 (提示：答案不惟一，如，，，等均可)．

[命题意图]考察学生进行几何图形的分解与组合，以及对几何图形进行简单变换的能力。考题渗透了“由简到繁”和“由易到难”的解题思想以及化归的思想方法。

7、给出下列四种图形：矩形、线段、等边三角形、正六边形．从对称性角度分析，其中与众不同的一种图形是　　　 。

[试题来源]自编

[参考答案]等边三角形

[命题意图]考察学生对轴对称以及中心对称图形掌握情况。

6、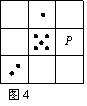现有3×3的方格，每个小方格内均有数目不同的点图，要求方格内每一行、每一列以及每一条对角线上的三个点图的点数之和均相等．图4中给出了部分点图，则P处所对应的点数是　　　　 　点　　　　　　　　　　　　　　　

][试题来源]自编

[参考答案]3

[命题意图]考察学生灵活运用方程知识解决问题的能力。考题巧妙地把“幻方”与“方程”以及“几何图形”结合在一起。

5、正方形ABCD在坐标系中的位置如图所示，将正方形ABCD绕D点顺时针旋转90°后，B点的坐标为(　 )

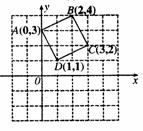
A、(－2，2)　 B、(4，1)　 C、(3，1)　 D、(4，0)

[试题来源]山东烟台08中考题

[参考答案]D

[命题意图]考察直角坐标系、正方形、解直角三角形、图形的旋转等知识点，以及“化动为静”解决问题的能力。考题巧妙地把正方形、解直角三角形、图形的旋转等知识点结合在直角坐标系这个平台中，并渗透“转化”这一最常见的数学思想方法。

4、如图2，已知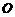为圆锥的顶点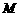，为圆锥底面上一点，点在上．一只蜗牛从点出发，绕圆锥侧面爬行，回到点时所爬过的最短路线的痕迹如下图所示．若沿将圆锥侧面剪开并展开，所得侧面展开图是　　　　　　　　　　　　　　　　　

[试题来源]北京08中考题

[参考答案]D

[命题意图]考察学生对于圆锥与圆锥侧面展开图掌握情况，以及空间想象能力。该题能创设问题情景，激发学生兴趣，使考题具有生活气息。

3、如图1、□ABCD中，E为AD的中点．已知△DEF的面积为S，则△DCF

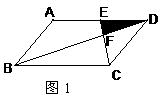的面积为　　　　　　　　　　　　　　　　　　　　　　　

A.S　　 　 B.2S　　　 C.3S　　 D.4S

[试题来源]自编

[参考答案]B

[命题意图]考察学生对于平行四边形性质、三角形的面积，相似三角形的判定与性质的运用情况，以及灵活应用知识的能力。考察的知识点多，覆盖面大。