
题目列表(包括答案和解析)
4.实数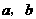 在数轴上对应点的位置如图所示,
在数轴上对应点的位置如图所示,
 则必有( )
则必有( )
A.和为正数 B.和为负数
C.积为正数 D. 积为负数
[命题意图]:①考察目的:此题主要考察学生对数轴上的点与有理数的对应关系的掌握,此外此题中还包含了有理数的的运算符号的确定。
②试题特色与亮点:把有理数的运算符号的确定与数轴相结合。
③测试后讲评,点a与点b表示的数分别在原点左右两侧且距离相等,则两数互为相反数,和为0,积为负。
[答案]:D [试题来源]:原创
3.如图所示的一组几何体的俯视图是( )



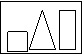

A. B. C. D.
[命题意图]:①考察目的:此题考查学生对三视图的掌握情况
②试题特色和亮点是:此题源自书本上的内容,让学生知道学习不能离开书本。
③测试后评讲,三视图时指对一个物体分别从三个方向看得到得平面图形的形状,从上面看的叫俯视图,从左面看的叫左视图,从右面看的叫右视图。
[答案]:C [试题来源]:原创
2.五名同学在为地震灾区的“爱心捐助”活动中,捐款数额为8,10,10,5,7(单位:元),这组数据的中位数是( )
A.10 B.8 C.9 D. 6
[命题意图]:①考察目的:此题主要考察学生对统计中的众数、中位数的理解与掌握的程度,。
②试题特色和亮点是:让学生在做题中体会一种“爱心”
③测试后评讲:此题要分清概念,知道什么是众数,中位数。中位数是指处在最中间位置的那个数或两个数的平均数。
[答案]:B [试题来源]原创
1.2009年4月22日北京新闻报道“自去年10月1日对外开放以来,北京‘鸟巢’共接待游客接近350万人次.” 350万这个数字用科学计数法表示为( )
A.3.5×10 B.3.5×10
B.3.5×10 C.3.5×10
C.3.5×10 D.35×10
D.35×10
[命题意图]:①考察目的:此题主要考察学生对科学计数法的掌握程度。
②试题特色和亮点是:此题与人们关心的北京奥运后的鸟巢现状相结合,让学生在轻松的环境中答题。
③测试后评讲:科学计数法要把一个数写成a×10 (1≤a<10 )的形式,其中350万=3500000,然后再用科学计数法表示。
(1≤a<10 )的形式,其中350万=3500000,然后再用科学计数法表示。
[答案]:C [试题来源]:原创
18、(1)已知 中,
中, ,
,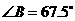 ,请画一条直线,把这个三角形分割成两个等腰三角形.(请你选用下面给出的备用图,把所有不同的分割方法都画出来.只需画图,不必说明理由,但要在图中标出相等两角的度数)
,请画一条直线,把这个三角形分割成两个等腰三角形.(请你选用下面给出的备用图,把所有不同的分割方法都画出来.只需画图,不必说明理由,但要在图中标出相等两角的度数)


(2)已知 中,
中, 是其最小的内角,过顶点
是其最小的内角,过顶点 的一条直线把这个三角形分割成了两个等腰三角形,请探求
的一条直线把这个三角形分割成了两个等腰三角形,请探求 与
与 之间的关系.
之间的关系.
[试题来源](2007无锡市中考题)
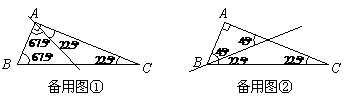
解:(1)如图(共有2种不同的分割法,)

(2)设 ,
, ,过点
,过点 的直线交边
的直线交边 于
于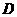 .在
.在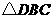 中,
中,
①若 是顶角,如图18-1,则
是顶角,如图18-1,则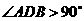 ,
,
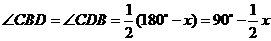 ,
, .
.
此时只能有 ,即
,即 ,
,
 ,即
,即 .
.
②若 是底角,则有两种情况.
是底角,则有两种情况.
第一种情况:如图18-2,当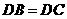 时,则
时,则 ,
,
 中,
中, ,
, .
.
1 .由
.由 ,得
,得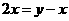 ,此时有
,此时有 ,即
,即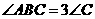 .
.
2 .由
.由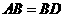 ,得
,得 ,此时
,此时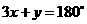 ,即
,即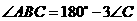 .
.
3 .由
.由 ,得
,得 ,此时
,此时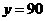
 ,即
,即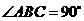 ,
, 为小于
为小于 的任意锐角.
的任意锐角.
第二种情况,如图18-3,当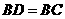 时,
时, ,
, ,此时只能有
,此时只能有 ,
,
从而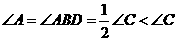 ,这与题设
,这与题设 是最小角矛盾.
是最小角矛盾.
 当
当 是底角时,
是底角时,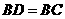 不成立.
不成立.


[命题意图]本题是一道压轴题,也是一道开放探索题。第(1)问是计算与作图相结合的探索。本问对学生运用作图工具的能力,以及运用直角三角形、等腰三角形性质等基础知识解决问题的能力都有较高的要求。第(2)问在第(1)问的基础上,由“特殊”到“一般”,“分类讨论”把直角三角形分成两个等腰三角形的各种情形并结合“方程思想”探究角与角之间的关系。本题不仅趣味性强,创造性强,而且渗透了由“特殊”到“一般”、“分类讨论”、“方程思想”、“转化思想”等数学思想,是一道不可多得的好题。
本资料由《七彩教育网》 提供!
17、如图,等腰梯形ABCD中,AB=4,CD=9,∠C=60°,动点P从点C出发沿CD方向向点D运动,动点Q同时以相同速度从点D出发沿DA方向向终点A运动,其中一个动点到达端点时,另一个动点也随之停止运动.
(1)求AD的长;
(2)设CP=x,问当x为何值时△PDQ的面积达到最大,并求出最大值;
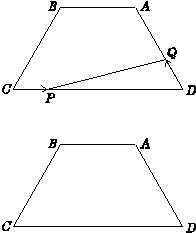 (3)探究:在BC边上是否存在点M使得四边形PDQM是菱形?若存在,请找出点M,并求出BM的长;不存在,请说明理由.
(3)探究:在BC边上是否存在点M使得四边形PDQM是菱形?若存在,请找出点M,并求出BM的长;不存在,请说明理由.
[试题来源]2008年龙岩市中考试
 题
题
[参考答案]
(1)解法一:如图17-1
过A作AE⊥CD,垂足为E .
依题意,DE=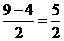 .
.
在Rt△ADE中,AD= .
.
 解法二:如图17-2
解法二:如图17-2
过点A作AE∥BC交CD于点E,则CE=AB=4 .
∠AED=∠C=60°.
又∵∠D=∠C=60°,
∴△AED是等边三角形 .
∴AD=DE=9-4=5 .
 2)解:如图17-1
2)解:如图17-1
∵CP=x,h为PD边上的高,依题意,
△PDQ的面积S可表示为:
S=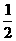 PD·h =
PD·h =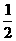 (9-x)·x·sin60°
(9-x)·x·sin60°
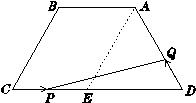 =
= (9x-x2) =-
(9x-x2) =- (x-
(x- )2+
)2+ . 由题意,
. 由题意,
知0≤x≤5 .
 当x=
当x= 时(满足0≤x≤5),S最大值=
时(满足0≤x≤5),S最大值= .
.
(3)证法一:如图17-3
 假设存在满足条件的点M,则PD必须等于DQ .
假设存在满足条件的点M,则PD必须等于DQ .
于是9-x=x,x= .
.
此时,点P、Q的位置如图25-3所示,
连QP。△PDQ恰为等边三角形 .
 过点Q作QM∥DC,交BC于M,点M即为所求.
过点Q作QM∥DC,交BC于M,点M即为所求.
连结MP,以下证明四边形PDQM是菱形 .
易证△MCP≌△QDP,∴∠D=∠3 . MP=PD
∴MP∥QD , ∴四边形PDQM是平行四边形 . 又MP=PD ,
∴四边形PDQM是菱形 。
所以存在满足条件的点M,且BM=BC-MC=5- =
=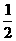 .
.
证法二:如图17-4存在满足条件的点M,则PD必须等于DQ .
于是9-x=x,x= .
.
此时,点P、Q的位置如图25-4所示,△PDQ恰为等边三角形 .
 过点D作DO⊥PQ于点O,延长DO交BC于点M,连结PM、QM,则DM垂直平分PQ,∴ MP=MQ .
过点D作DO⊥PQ于点O,延长DO交BC于点M,连结PM、QM,则DM垂直平分PQ,∴ MP=MQ .
易知∠1=∠C .
∴PQ∥BC .
又∵DO⊥PQ, ∴MC⊥MD
 ∴MP=
∴MP= 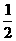 CD=PD
CD=PD
即MP=PD=DQ=QM
∴四边形PDQM是菱形
所以存在满足条件的点M,且BM=BC-MC=5- =
=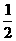
[命题意图]本题是一道压轴题,也是一道开放探索题,第(2)问是条件开放,第(3)问是结论开放。本题既考察了学生的分析作图能力,又考察学生综合运用平行线、等腰梯形、等边三角形、菱形、二次函数等知识。这里设计了一个开放的、动态的数学情境,为学生灵活运用基础知识、分析问题、解决问题留下了广阔的探索、创新的思维空间。
15、一枚均匀的正方体骰子,六个面分别标有数字1,2,3,4,5,6.如果用小刚抛掷正方体骰子朝上的数字 ,小强抛掷正方体骰子朝上的数字
,小强抛掷正方体骰子朝上的数字 来确定点
来确定点 ,那么他们各抛掷一次所确定的点
,那么他们各抛掷一次所确定的点 落在已知直线
落在已知直线 图象上的概率是多少?
图象上的概率是多少?
[试题来源]青海省西宁市2008年高中试题
[参考答案]解:由题意可得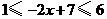 ,化为不等式组
,化为不等式组 解得
解得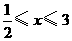 。
。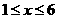 ,且
,且 为正整数,
为正整数,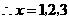 .要使点
.要使点 落在直线
落在直线 图象上,则对应的
图象上,则对应的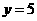 ,3,1 。
,3,1 。 满足条件的点
满足条件的点 有(1,5),(2,3),(3,1)抛掷骰子所得
有(1,5),(2,3),(3,1)抛掷骰子所得 点的总个数为36.
点的总个数为36.  点
点 落在直线
落在直线 图象上的概率
图象上的概率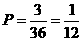 。答:点
。答:点 落在直线
落在直线 图象上的概率是
图象上的概率是 .
.
[命题意图]本题巧妙地把概率、不等式组、一次函数等知识结合在一起,出题思路新颖,别具一格。有利于考察学生灵活应用基础知识解决问题的能力。
14、振兴中学某班的学生对本校学生会倡导的“抗震救灾,众志成城”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.下图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3︰4︰5︰8︰6,又知此次调查中捐款25元和30元的学生一共42人.
(1)他们一共调查了多少人? (2)这组数据的众数、中位数各是多少?
(3)若该校共有1560名学生,估计全校学生捐款多少元?

[试题来源]2009 年山东莱芜中考题
[参考答案]解:(1)设捐款30元的有6x人,则8x+6x=42.
∴ x=3.∴ 捐款人数共有:3x+4x+5x+8x+6x=78(人).
(2)由图象可知:众数为25(元);由于本组数据的个数为78,按大小顺序
排列处于中间位置的两个数都是25(元),故中位数为25(元). (3) 全校共捐款:
(9×10+12×15+15×20+24×25+18×30)×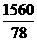 =34200(元).
=34200(元).
[命题意图]本题是一道把统计知识与实际生活中的问题联系起来的应用题,以考察学生处理数据的能力,使学生初步体会统计知识与生活、社会和科技的联系,感受数学应用的意义。培养学生自觉应用数学知识解决实际问题的能力。
13、如图,在 中,
中,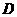 是
是 边上的一点,
边上的一点,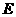 是
是 的中点,过点
的中点,过点 作
作 的平行线交
的平行线交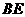 的延长线于
的延长线于 ,且
,且 ,连接
,连接 .
.
(1)求证: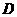 是
是 的中点;
的中点;
(2)如果 ,试猜测四边形
,试猜测四边形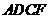 的形状,并证明你的结论.
的形状,并证明你的结论.
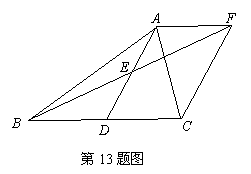
[试题来源]青海省2008年中考考试数学试卷
[参考答案]
(1)证明: ,
, 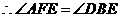 .
.  是
是 的中点,
的中点,  .又
.又 ,
, 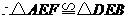 .
.  .
.  ,
,  .
.
即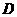 是
是 的中点.(2)解:四边形
的中点.(2)解:四边形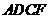 是矩形证明:
是矩形证明: ,
, ,
,
 四边形
四边形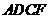 是平行四边形.
是平行四边形.  ,
,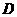 是
是 的中点,
的中点, 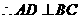 .
.
即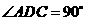 .
.  四边形
四边形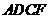 是矩形.
是矩形.
[命题意图]此题是一道几何结论开放题,可以大大激发学生的思考兴趣,拓展学生的思维空间,培养学生求异、求变的创新精神。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com