2.待定系数法确定正比例函数、一次函数的解析式：通常已知一点便可用待定系数法确定出正比例函数的解析式，已知两点便可确定一次函数解析式。

1.正比例函数与一次函数的关系：正比例函数是当y=kx+b中b=0时特殊的一次函数。

8．(1)已知：如图①，BD、CE分别是△ABC的外角平

分线，过点A作AF⊥BD，AG⊥CE，垂足分别是

F、G，连结FG，延长AF、AG，与直线BC相交．

求证：FG= (AB+BC+AC)．

(2)若BD、CE分别是△ABC的内角平分线，其余条件不变

(如图②)，线段FG与△ABC的三边又有怎样的数量关系?

写出你的猜想，并给予证明．

7．在直角坐标系中，已知A(-4，0)、

B(1，0)、C(0，-2)三点．请按以

下要求设计两种方案：作一条与

轴不重合，与△ABC的两边相

交的直线，使截得的三角形与

△ABC相似，并且面积是△AOC

面积的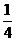．分别在下面的两个坐标中系画出设计图形，并写出截得的三角形三个顶点的坐标．

6．如图()所示，锐角△ABC中，BC>AB>AC，D、E分别是BC、AB上的动点，连结

AD、DE．

(1)当D、E运动时，分别在其余的三个图中画出D、E运动的位置；在图(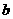)中画出仅有一组三角形相似的图形；在图()中画出仅有二组三角形相似的图形；在图()中画出有三组三角形相似的图形．

(2)BC=9，AB=8，AC=6，就图()求出DE的长．

5．如图，已知，△ABC、△DCE、△FEG是三个全等的等腰

三角形，底边BC、CE、EG在同一直线上，且AB=，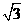

BC=1．连结BF，分别交AC、DC、DE于点P、Q、R．

(1)△BFG与△FEG相似吗?为什么?

(2)写出图中所有与△ABP相似的三角形(不必证明)．

4．如图，正方形网格中的小正方形的面积都为1，

网格中有△ABC和△DFE．

(1)这两个三角形相似吗?说出你的理由；

(2)请你以网格中的格点为顶点，在网格中再画出

一个面积为4且与△ABC相似的三角形．

3．测量小玻璃管口径的量具CDE上，CD=l0mm，

DE=80mm．如果小管口径AB正对着量具上的

50mm刻度，那么小管口径AB的长是多少?

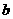2．如图，有一湖泊，岸边A、B间的距离不能直接测量，为得到A、B间的距离，请你利用测角仪和皮量尺，在岸上设计出两种测量方案(分别画出说明方案的图形，方案的依据需是本单元的有关知识)，并就方案写出表示A、B间的距离的所要测量的线段．(经测量所得线段长用 (或或等)表示，角度用α(或β)表示)．

1．在如图所示的方格纸中，画出，△DEF和△DEG

(F、G不能重合)，使得△ABC≌△DEF≌DEG．

你能说明它们为什么全等吗?

‘’