
题目列表(包括答案和解析)
9、(临沂市08)已知∠MAN,AC平分∠MAN。
⑴在图1中,若∠MAN=120°,∠ABC=∠ADC=90°,求证:AB+AD=AC;
⑵在图2中,若∠MAN=120°,∠ABC+∠ADC=180°,则⑴中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
⑶在图3中:
①若∠MAN=60°,∠ABC+∠ADC=180°,则AB+AD=____AC;
 ②若∠MAN=α(0°<α<180°),∠ABC+∠ADC=180°,则AB+AD=____AC(用含α的三角函数表示),并给出证明。
②若∠MAN=α(0°<α<180°),∠ABC+∠ADC=180°,则AB+AD=____AC(用含α的三角函数表示),并给出证明。
8、(2008年益阳) 两个全等的直角三角形ABC和DEF重叠在一起,其中∠A=60°,AC=1. 固定△ABC不动,将△DEF进行如下操作:
(1) 如图8(1),△DEF沿线段AB向右平移(即D点在线段AB内移动),连结DC、CF、FB,四边形CDBF的形状在不断的变化,但它的面积不变化,请求出其面积.

(2)如图8(2),当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明理由.

(3)如图8(3),△DEF的D点固定在AB的中点,然后绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,连结AE,请你求出sinα的值.

7、(2005年武汉市)将两块含30°角且大小相同的直角三角板如图1摆放。
 (1)将图1中△
(1)将图1中△ 绕点C顺时针旋转45°得图2,点
绕点C顺时针旋转45°得图2,点 与AB的交点,求证:
与AB的交点,求证: ;
;
(2)将图2中△ 绕点C顺时针旋转30°到△
绕点C顺时针旋转30°到△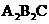 (如图3),点
(如图3),点 与AB的交点。线段
与AB的交点。线段 之间存在一个确定的等量关系,请你写出这个关系式并说明理由;
之间存在一个确定的等量关系,请你写出这个关系式并说明理由;

(3)将图3中线段 绕点C顺时针旋转60°到
绕点C顺时针旋转60°到
(如图4),连结 ,求证:
,求证: ⊥AB.
⊥AB.
6、(08河北)如图14-1, 的边
的边 在直线
在直线 上,
上, ,且
,且 ;
; 的边
的边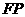 也在直线
也在直线 上,边
上,边 与边
与边 重合,且
重合,且 .
.
(1)在图14-1中,请你通过观察、测量,猜想并写出 与
与 所满足的数量关系和位置关系;
所满足的数量关系和位置关系;
(2)将 沿直线
沿直线 向左平移到图14-2的位置时,
向左平移到图14-2的位置时, 交
交 于点
于点 ,连结
,连结 ,
, .猜想并写出
.猜想并写出 与
与 所满足的数量关系和位置关系,请证明你的猜想;
所满足的数量关系和位置关系,请证明你的猜想;
(3)将 沿直线
沿直线 向左平移到图14-3的位置时,
向左平移到图14-3的位置时, 的延长线交
的延长线交 的延长线于点
的延长线于点 ,连结
,连结 ,
, .你认为(2)中所猜想的
.你认为(2)中所猜想的 与
与 的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.
的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.


5、(武汉07)填空或解答:点B、C、E在同一直线上,点A、D在直线CE的同侧,AB=AC,EC=ED,∠BAC=∠CED,直线AE、BD交于点F。
(1)如图①,若∠BAC=60°,则∠AFB=_________;如图②,若∠BAC=90°,则∠AFB=_________;
(2)如图③,若∠BAC=α,则∠AFB=_________(用含α的式子表示);
 (3)将图③中的△ABC绕点C旋转(点F不与点A、B重合),得图④或图⑤。在图④中,∠AFB与∠α的数量关系是________________;在图⑤中,∠AFB与∠α的数量关系是________________。请你任选其中一个结论证明。
(3)将图③中的△ABC绕点C旋转(点F不与点A、B重合),得图④或图⑤。在图④中,∠AFB与∠α的数量关系是________________;在图⑤中,∠AFB与∠α的数量关系是________________。请你任选其中一个结论证明。

4、(08荆门)将两块全等的含30°角的三角尺如图(1)摆放在一起,它们的较短直角边长为3.(1) 将△ECD沿直线l向左平移到图(2)的位置,使E点落在AB上,则CC′=______;
(2) 将△ECD绕点C逆时针旋转到图(3)的位置,使点E落在AB上,则△ECD绕点C旋转的度数=______;
(3) 将△ECD沿直线AC翻折到图(4)的位置,ED′与AB相交于点F,求证AF=FD′


3、(07河北| )在△ABC中,AB=AC,CG⊥BA交BA的延长线于点G.一等腰直角三角尺按如图15-1所示的位置摆放,该三角尺的直角顶点为F,一条直角边与AC边在一条直线上,另一条直角边恰好经过点B.
)在△ABC中,AB=AC,CG⊥BA交BA的延长线于点G.一等腰直角三角尺按如图15-1所示的位置摆放,该三角尺的直角顶点为F,一条直角边与AC边在一条直线上,另一条直角边恰好经过点B.
(1)在图15-1中请你通过观察、测量BF与CG的
长度,猜想并写出BF与CG满足的数量关系,
然后证明你的猜想;
(2)当三角尺沿AC方向平移到图15-2所示的位置时,
一条直角边仍与AC边在同一直线上,另一条
直角边交BC边于点D,过点D作DE⊥BA于
点E.此时请你通过观察、测量DE、DF与CG
的长度,猜想并写出DE+DF与CG之间满足
的数量关系,然后证明你的猜想;
(3)当三角尺在(2)的基础上沿AC方向继续平
移到图15-3所示的位置(点F在线段AC上,
且点F与点C不重合)时,(2)中的猜想是否
仍然成立?(不用说明理由)
2、(06河北)如图13-1,一等腰直角三角尺GEF的两条直角边与正方形ABCD的两条边分别重合在一起.现正方形ABCD保持不动,将三角尺GEF绕斜边EF的中点O(点O也是BD中点)按顺时针方向旋转.
(1)如图13-2,当EF与AB相交于点M,GF与BD相交于点N时,通过观察或测量BM,FN的长度,猜想BM,FN满足的数量关系,并证明你的猜想;

 (2)若三角尺GEF旋转到如图13-3所示的位置时,线段FE的延长线与AB的延长线相交于点M,线段BD的延长线与GF的延长线相交于点N,此时,(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.
(2)若三角尺GEF旋转到如图13-3所示的位置时,线段FE的延长线与AB的延长线相交于点M,线段BD的延长线与GF的延长线相交于点N,此时,(1)中的猜想还成立吗?若成立,请证明;若不成立,请说明理由.

1、(04河北)用两个全等的等边三角形△ABC和△ACD拼成菱形ABCD.把一个含60°角的三角尺与这个菱形叠合,使三角尺的60°角的顶点与点A重合,两边分别与AB,AC重合.将三角尺绕点A按逆时针方向旋转.
 (1)当三角尺的两边分别与菱形的两边BC,CD相交于点E,F时,(如图13-1),通过观察或测量BE,CF的长度,你能得出什么结论?并证明你的结论;
(1)当三角尺的两边分别与菱形的两边BC,CD相交于点E,F时,(如图13-1),通过观察或测量BE,CF的长度,你能得出什么结论?并证明你的结论;
 (2)当三角尺的两边分别与菱形的两边BC,CD的延长线相交于点E,F时(如图13-2),你在(1)中得到的结论还成立吗?简要说明理由.
(2)当三角尺的两边分别与菱形的两边BC,CD的延长线相交于点E,F时(如图13-2),你在(1)中得到的结论还成立吗?简要说明理由.
10.(08枣庄)如图,在直角坐标系中放入一个边长OC为9的矩形纸片ABCO.将纸片翻折后,点B恰好落在x轴上,记为B′,折痕为CE,已知tan∠OB′C= .
.
 (1)求B′点的坐标;
(1)求B′点的坐标;
(2)求折痕CE所在直线的解析式.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com