
题目列表(包括答案和解析)
5.求抛物线的顶点、对称轴的方法
(1)公式法: ,∴顶点是
,∴顶点是 ,对称轴是直线
,对称轴是直线 .
.
(2)配方法:运用配方的方法,将抛物线的解析式化为 的形式,得到顶点为(
的形式,得到顶点为( ,
, ),对称轴是直线
),对称轴是直线 .
.
(3)运用抛物线的对称性:由于抛物线是以对称轴为轴的轴对称图形,所以对称轴的连线的垂直平分线是抛物线的对称轴,对称轴与抛物线的交点是顶点.用配方法求得的顶点,再用公式法或对称性进行验证,才能做到万无一失.
4.顶点决定抛物线的位置.几个不同的二次函数,如果二次项系数 相同,那么抛物线的开口方向、开口大小完全相同,只是顶点的位置不同.
相同,那么抛物线的开口方向、开口大小完全相同,只是顶点的位置不同.
3.抛物线的三要素:开口方向、对称轴、顶点.
① 的符号决定抛物线的开口方向:当
的符号决定抛物线的开口方向:当 时,开口向上;当
时,开口向上;当 时,开口向下;
时,开口向下;
 相等,抛物线的开口大小、形状相同.
相等,抛物线的开口大小、形状相同.
②平行于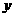 轴(或重合)的直线记作
轴(或重合)的直线记作 .特别地,
.特别地,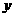 轴记作直线
轴记作直线 .
.
2.二次函数 用配方法可化成:
用配方法可化成: 的形式,其中
的形式,其中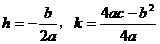 .
.
1.定义:一般地,如果 是常数,
是常数, ,那么
,那么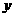 叫做
叫做 的二次函数.
的二次函数.
2、某服装经销商,库存有进价每套400元的A品牌服装1200套,正常销售时每套600元,一年内刚好买完。现在市场上流行B品牌服装,此进价每套200元,售出价每套500元,肯定比A产品销售套数多(两种服装的市场行情互不受影响)。目前有一可进B品牌服装的机会,若这一机会错过,估计一年内进步到这种服装,可是,该经销商苦于手头无流动资金可用,只有低价将部分A品牌服装转让该另一经销商。转让价格(元/套)与转让数量(套)有如下关系:
|
转让数量(套) |
1200 |
1100 |
1000 |
900 |
800 |
700 |
600 |
500 |
400 |
300 |
200 |
100 |
|
价格(元/套) |
240 |
250 |
260 |
270 |
280 |
290 |
300 |
310 |
320 |
330 |
340 |
350 |
(1) 设转让数量为x套,转让的单价为每套y元,判断y与x函数关系,求出y与x函
数关系式。
(2)
求销售A品牌服装一年获利 与x函数关系式,销售B品牌服装一年获
与x函数关系式,销售B品牌服装一年获 利与x
利与x
函数关系式。
(3)该经销商转让多少套A品牌服装,使其一年内获利最多?
(09桥西模拟)某种产品的年产量不超过1000吨,该产品的费用 (单位:万元)与年产量x之间的函数图像是顶点在原点的抛物线的一部分,如图,该产品的销售单价
(单位:万元)与年产量x之间的函数图像是顶点在原点的抛物线的一部分,如图,该产品的销售单价 (单位:万元/吨)与每年销售量x(单位:吨)之间的关系如下表所示:
(单位:万元/吨)与每年销售量x(单位:吨)之间的关系如下表所示:
|
年销售量x(吨) |
0 |
200 |
400 |
﹍ |
1000 |
销售单价 (万元/吨) (万元/吨) |
30 |
28 |
26 |
﹍ |
20 |
 (1)求出
(1)求出 与年产量x(吨)之间的函数关系式;
与年产量x(吨)之间的函数关系式;
(2)求出 与年销售量x(吨)之间的函数关系式;
与年销售量x(吨)之间的函数关系式;
(3)若生产出的产品都能在当年售完,求出利润w(万元)与年产量x之间的函数关系式;并求出最佳生产销售方案时的年产量和单价。
(4)画出W与x的函数图像草图,由图像回答,与销售单价为23万元/吨时,利润相同的单价还有哪个单价?
(模拟改编)我市宣化素有“葡萄之乡”著称,某葡萄园有100株葡萄秧,每株平均产量为40千克,现准备多种一些以提高产量,但是如果多种葡萄秧,那么每株之间的距离和每株葡萄秧接受的阳光就会减少。根据实践经验,增加的株数与每株葡萄秧的产量之间的关系如下表所示:
|
增加的株数x(株) |
… |
10 |
15 |
20 |
22 |
… |
|
每株葡萄秧的产量y(千克) |
… |
37.5 |
36.25 |
35 |
34.5 |
… |
(1) 请你用所学过的只是确定一个y与x之间的函数关系式;
(2) 在(1)的条件下,求葡萄园的总产量P与x的函数关系式;
(3) 在(1)的条件下,当增种多少株葡萄秧时,葡萄园的总产量最多?
(4) 在实际运作中,为充分利用冷库资源,此葡萄园的产量不能低于4200千克,请利用函数图像,确定增种葡萄株数的范围。
(七中09模拟)某地区盛产一特农产品,经过市场调查,发现该产品在A市有很好的消费市场,于是2008年该公司以9万元/吨的市场保护价收购该产品,收购产品、分类包装、运往A市等费用约为0.5万元/吨,所收购产品的损耗率5%,在A市销售价为15万元/吨。
2009年公司在收购价与销售价不变的前提下,准备拿出一定的资金在A市做广告宣传。据调查投入广告费为x(万元)与在2008年销量的基础上该产品的销量y(吨)之间满足y=ax²+bx+50, 并且当投1万元的广告费时,销量为59吨;当投入2万元的广告费时,销量66吨。
⑴公司2008年将销售利润全部回报农民,在市场保护价的基础上,农民每卖出1千克的产品还可增收 47.5 元?
⑵试写出y与x间的函数关系式,并根据关系式可知,2008年公司实际收购产品吨
⑶设2009年公司的销售利润为W(万元))(销售利润=销售额-成本费-广告费),试写出W与x之间的二次函数关系式:
⑷将⑶中所求二次函数关系式化成y=a(x+)²+
的形式,并据此说明当广告费定为多少万元时,2009年公司的销售利润最大?最大利润为多少?
W=15y-(y÷95%)(9+0.5)-x
 (08泰安市)某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数
(08泰安市)某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数 (亩)与补贴数额
(亩)与补贴数额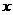 (元)之间大致满足如图1所示的一次函数关系.随着补贴数额
(元)之间大致满足如图1所示的一次函数关系.随着补贴数额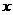 的不断增大,出口量也不断增加,但每亩蔬菜的收益
的不断增大,出口量也不断增加,但每亩蔬菜的收益 (元)会相应降低,且
(元)会相应降低,且 与
与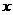 之间也大致满足如图2所示的一次函数关系.
之间也大致满足如图2所示的一次函数关系.
(1)在政府未出台补贴措施前,该市种植这种蔬菜的总收益额为多少?
(2)分别求出政府补贴政策实施后,种植亩数 和每亩蔬菜的收益
和每亩蔬菜的收益 与政府补贴数额
与政府补贴数额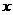 之间的函数关系式;
之间的函数关系式;
(3)要使全市这种蔬菜的总收益 (元)最大,政府应将每亩补贴数额
(元)最大,政府应将每亩补贴数额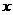 定为多少?并求出总收益
定为多少?并求出总收益 的最大值.
的最大值.
35、 (09河北中考说明示例)某公司年初推出一种高新技术产品,该产品销售的累积利润y(万元)与销售时间x(月)之间的关系(即前x个月的利润总和y与x之间的关系)为y=
(09河北中考说明示例)某公司年初推出一种高新技术产品,该产品销售的累积利润y(万元)与销售时间x(月)之间的关系(即前x个月的利润总和y与x之间的关系)为y= (x>0).
(x>0).
(1)求出这个函数图像的顶点坐标和对称轴;
(2)请在如图所给坐标系中,画出这个函数图像的简图;
(3)根据函数图像,你能否判断出公司的这种新产
品销售累积利润是从什么时间开始盈利的?
(4)这个公司第6个月所获的利润是少?
 (08梅州)如图11所示,在梯形ABCD中,已知AB∥CD, AD⊥DB,AD=DC=CB,AB=4.以AB所在直线为x轴,过D且垂直于AB的直线为y轴建立平面直角坐标系.(1)求∠DAB的度数及A、D、C三点的坐标;(2)求过A、D、C三点的抛物线的解析式及其对称轴L.(3)若P是抛物线的对称轴L上的点,那么使
(08梅州)如图11所示,在梯形ABCD中,已知AB∥CD, AD⊥DB,AD=DC=CB,AB=4.以AB所在直线为x轴,过D且垂直于AB的直线为y轴建立平面直角坐标系.(1)求∠DAB的度数及A、D、C三点的坐标;(2)求过A、D、C三点的抛物线的解析式及其对称轴L.(3)若P是抛物线的对称轴L上的点,那么使 PDB为等腰三角形的点P有几个?(不必求点P的坐标,只需说明理由)
PDB为等腰三角形的点P有几个?(不必求点P的坐标,只需说明理由)
34、(09河北中考说明示例)行驶中的玩具模型汽车如果制动,由于惯性作用,制动后还要向前滑行一段距离才能停止,称这段距离为玩具模型汽车“刹车距离”。小静购了某型号的玩具汽车,他通过多次刹车实验,得到该玩具车的刹车距离 l (米)与车速x(米/秒)之间大致满足二次函数关系: l = 根据图中提供的数据,回答下列问题:
根据图中提供的数据,回答下列问题:
(1) 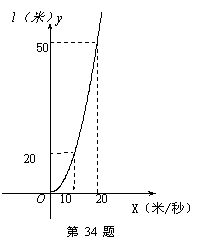 确定刹车距离 l (米)与车速x(米/秒)
确定刹车距离 l (米)与车速x(米/秒)
的函数解析式。
(2) 
|
 小静在操作玩具汽车游戏时,突然发现
小静在操作玩具汽车游戏时,突然发现
正前方10米处有障碍物,小静从发现有障碍物
到作出刹车制动反应用了0.5秒的时间,结果在
距离障碍物1.2米处将车停止,问玩具汽车制动
前的速度为每秒多少米?
33、(海南08)如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在射线BC上,且PE=PB.
 (1)求证:① PE=PD ; ② PE⊥PD;
(1)求证:① PE=PD ; ② PE⊥PD;
(2)设AP=x, △PBE的面积为y.
① 求出y关于x的函数关系式,并写出x的取值范围;
② 当x取何值时,y取得最大值,并求出这个最大值.
32、(长春07)如图①,在Rt△ABC中,∠C=90°,边BC的长为20cm,边AC的长为hcm,在此三角形内有一个矩形CFED,点D、E、F分别在AC、AB、BC上,设AD的长为xcm,矩形CFED的面积为y(单位:cm2).
(1)当h等于30时,求y与x的函数关系式(不要求写出自变量x的取值范围);
(2)在(1)的条件下,矩形CFED的面积能否为180cm2?请说明理由;
(3)若y与x的函数图象如图②所示,求此时h的值.
(参考公式:二次函数y=ax2+bx+c,当 时,y最大(小)值=
时,y最大(小)值=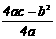 .)
.)

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com