
题目列表(包括答案和解析)
18、(金华08 )如图1,已知双曲线y=
)如图1,已知双曲线y= (k>0)与直线y=k′x交于A,B两点,点A在第一象限.试解答下列问题:(1)若点A的坐标为(4,2).则点B的坐标为 ;若点A的横坐标为m,则点B的坐标可表示为 ;(2)如图2,过原点O作另一条直线l,交双曲线y=
(k>0)与直线y=k′x交于A,B两点,点A在第一象限.试解答下列问题:(1)若点A的坐标为(4,2).则点B的坐标为 ;若点A的横坐标为m,则点B的坐标可表示为 ;(2)如图2,过原点O作另一条直线l,交双曲线y= (k>0)于P,Q两点,点P在第一象限.①说明四边形APBQ一定是平行囚边形;②设点A.P的横坐标分别为m,n,四边形APBQ可能是矩形吗?可能是正方形吗?若可能,直接写出m、n应满足的条件;若不可能,请说明理由.
(k>0)于P,Q两点,点P在第一象限.①说明四边形APBQ一定是平行囚边形;②设点A.P的横坐标分别为m,n,四边形APBQ可能是矩形吗?可能是正方形吗?若可能,直接写出m、n应满足的条件;若不可能,请说明理由.
17、 (08德州)(1)探究新知:如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由.
(08德州)(1)探究新知:如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由.
(2)结论应用:① 如图2,点M,N在反比例函数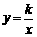 (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F. 试证明:MN∥EF.
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F. 试证明:MN∥EF.
② 若①中的其他条件不变,只改变点M,N 的位置如图3所示,请判断 MN与EF是否平行.
16、(08南通)已知双曲线 与直线
与直线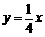 相交于A、B两点.第一象限上的点M(m,
相交于A、B两点.第一象限上的点M(m,
n)(在A点左侧)是双曲线 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,
-n)作NC∥x轴交双曲线 于点E,交BD于点C.
于点E,交BD于点C.
(1)若点D坐标是(-8,0),求A、B两点坐标及k的值.
(2)若B是CD的中点,四边形OBCE的面积为4,求直线CM的解析式.
 (3)设直线AM、BM分别与y轴相交于P、Q两点,且MA=pMP,MB=qMQ,求p-q的值.
(3)设直线AM、BM分别与y轴相交于P、Q两点,且MA=pMP,MB=qMQ,求p-q的值.
15、( 08杭州)为了预防流感,某学校在休息天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量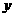 (毫克)与时间
(毫克)与时间 (小时)成正比;药物释放完毕后,
(小时)成正比;药物释放完毕后,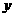 与
与 的函数关系式为
的函数关系式为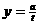 (
(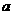 为常数),如图所示.据图中提供的信息,解答下列问题:
为常数),如图所示.据图中提供的信息,解答下列问题:
(1)
写出从药物释放开始,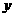 与
与 之间的两个函数关系式及相应的自变量的取值范围;
之间的两个函数关系式及相应的自变量的取值范围;
 (第15题) |
(2)据测定,当空气中每立方米的含药量降低到 毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?
毫克以下时,学生方可进入教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?
14、(镇江08)如图,奥运圣火抵达某市奥林匹克广场后,沿图中直角坐标系中的一段反比例函数图象传递.动点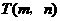 表示火炬位置,火炬从离北京路10米处的
表示火炬位置,火炬从离北京路10米处的 点开始传递,到离北京路1000米的
点开始传递,到离北京路1000米的 点时传递活动结束.迎圣火临时指挥部设在坐标原点
点时传递活动结束.迎圣火临时指挥部设在坐标原点 (北京路与奥运路的十字路口),
(北京路与奥运路的十字路口), 为少先队员鲜花方阵,方阵始终保持矩形形状且面积恒为10000平方米(路线宽度均不计).
为少先队员鲜花方阵,方阵始终保持矩形形状且面积恒为10000平方米(路线宽度均不计).
(1)求图中反比例函数的关系式(不需写出自变量的取值范围);
(2)当鲜花方阵的周长为500米时,确定此时火炬的位置(用坐标表示);
(3)设 ,用含
,用含 的代数式表示火炬到指挥部的距离;当火炬离指挥部最近时,确定此时火炬的位置(用坐标表示).
的代数式表示火炬到指挥部的距离;当火炬离指挥部最近时,确定此时火炬的位置(用坐标表示).

13、(07福州)如图,已知直线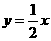 与双曲线
与双曲线 交于
交于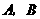 两点,且点
两点,且点 的横坐标为
的横坐标为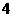 .
.
(1)求 的值;
的值;
(2)若双曲线 上一点
上一点 的纵坐标为8,求
的纵坐标为8,求 的面积;
的面积;
 (3)过原点
(3)过原点 的另一条直线
的另一条直线 交双曲线
交双曲线 于
于 两点(
两点( 点在第一象限),若由点
点在第一象限),若由点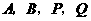 为顶点组成的四边形面积为
为顶点组成的四边形面积为 ,求点
,求点 的坐标.
的坐标.
12、(07呼和浩特)如图,已知反比例函数 的图象与一次函数
的图象与一次函数 的图象交于
的图象交于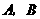 两点,
两点,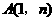 ,
, .
.
(1)求反比例函数和一次函数的解析式;
 (2)在
(2)在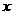 轴上是否存在点
轴上是否存在点 ,使
,使 为等腰三角形?若存在,请你直接写出
为等腰三角形?若存在,请你直接写出 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
11、(08资阳)若一次函数y=2x-1和反比例函数y= 的图象都经过点(1,1).
的图象都经过点(1,1).
(1)求反比例函数的解析式;
(2)已知点A在第三象限,且同时在两个函数的图象上,求点A的坐标;
(3)利用(2)的结果,若点B的坐标为(2,0),且以点A、O、B、P为顶点的四边形是平行四边形,请你直接写出点P的坐标.
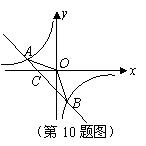
10、(南充08)如图,已知 ,
, 是一次函数
是一次函数 的图像和反比例函数
的图像和反比例函数 的图像的两个交点.
的图像的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)根据图像写出使一次函数的值小于反比例函数值的x的取值范围;
 (3)求直线
(3)求直线 与
与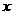 轴的交点
轴的交点 的坐标及三角形
的坐标及三角形 的面积.
的面积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com