2. 用换元法解方程　 原方程化为关于y的一元二次方程是____________。

1. 分解因式　 ______________________。

5. 已知两圆的半径分别为2cm、5cm，两圆有且只有三条公切线，则它们的圆心距一定(　　 )

　　 A. 大于3cm且小于7cm　　　 B. 大于7cm　　　　　　　　 　　 C. 等于3cm　　　　　　　　　　　　 D. 等于7cm

4. 下列图形中，是轴对称图形但不是中心对称图形的是(　　 )

　　 A. 平行四边形　　　　　　　　　 B. 菱形　　　　　　　　　　　 　　 C. 直角梯形　　　　　　　　　　　 D. 等边三角形

3. 对二次函数进行配方，其结果及顶点坐标是(　　 )

　　 A. 　　　　　　　　　　　　　　 B.

　　 C. 　　　　　　　　　　　　　　　　 D.

2. 为适应经济的发展，提高铁路运输能力，铁道部决定提高列车运行的速度，甲、乙两城市相距300千米，客车的行车速度每小时比原来增加了40千米，因此，从甲市到乙市运行的时间缩短了1小时30分，若设客车原来的速度为每小时x千米，则依题意列出的方程是(　　 )

　　 A. 　　　　　　　　　　　　　　　　　　　　　　　　 B.

　　 C. 　　　　　　　　　　　　　　　　　　　　　　　　 D.

1. 在下列二次根式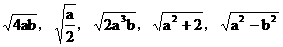中，最简二次根式有(　　 )

　　 A. 1个　　　　　　　　　　　　　　　　 B. 2个　　　　　　　　　　　　　　　　　　　　 C. 3个　　　　　　　　　　　　　　　　　　　　 D. 4个

11. 如图所示，在△ABC中，∠B=90°，AB=6厘米，BC=3厘米，点P从点A开始沿AB边向B以1厘米/秒的速度移动，点Q从点B开始沿BC边向点C以2厘米/秒的速

米？(把实际问题转化为几何问题)

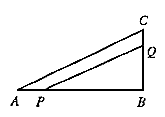
　　 解：

　　 提示：

的左侧)的横坐标的平方和为10。

　　 (1)求此抛物线的解析式。

　　 *(2)若Q是抛物线上异于A、B、P的点，且∠QAP=90°，求点Q的坐标。(利用“点坐标的绝对值等于线段长”沟通函数与几何，转化为点坐标用函数知识，转化为线段长用几何知识)

　　 解：(1)

　　 提示：∵顶点P在直线y＝－4x上，

　　 ∴P(1，－4)或(－1，4)。

　　 ∵抛物线开口向上，又与x轴有交点，

　　 ∴(－1，4)不合题意舍去。

　　 (2)

　　 提示：如图所示，设抛物线上点Q(m，n)，过Q作QP⊥x轴于点M。

　　 ∵∠QAP=90°，

　　 由勾股定理，得

函数知识，视为方程的根用方程知识)。

　　 解：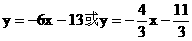

　　 提示：

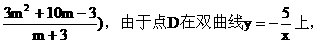
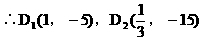
　　 其中C₁(2，1)不符合题意，舍去。

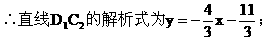
10. 如图所示，以正方形ABCD平行于边的对称轴为坐标轴建立直角坐标系，若正方形的边长为4。

　　 (1)求过B、E、F三点的二次函数的解析式；

　　 (2)求此抛物线的顶点坐标。

　　 (先转化为点的坐标，再求函数解析式)

　　 解：(1)

　　 提示：点B(－2，－2)，点E(0，2)，点F(2，0)；

　　 (2)

9. △ABC中，AD是高，AD与AB的夹角为锐角α，Rt△ABC的面积和周长都为

“代数式”作为方程的系数)

　　 解：(1)

　　 提示：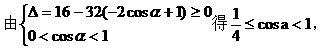

　　 (2)

　　 提示：