
题目列表(包括答案和解析)
4.(•杭州市)在直角坐标系xOy中,设点A(0,t),点Q(t,b)。平移二次函数 的图象,得到的抛物线F满足两个条件:①顶点为Q;②与x轴相交于B,C两点(∣OB∣<∣OC∣),连结A,B。
的图象,得到的抛物线F满足两个条件:①顶点为Q;②与x轴相交于B,C两点(∣OB∣<∣OC∣),连结A,B。
(1)是否存在这样的抛物线F,使得 ?请你作出判断,并说明理由;
?请你作出判断,并说明理由;
(2)如果AQ∥BC,且tan∠ABO=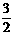 ,求抛物线F对应的二次函数的解析式。
,求抛物线F对应的二次函数的解析式。

第2课时 函数型问题 答案
3.(·贵阳市)某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间可以住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用.
设每个房间每天的定价增加 元.求:
元.求:
(1)房间每天的入住量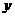 (间)关于
(间)关于 (元)的函数关系式.
(元)的函数关系式.
(2)该宾馆每天的房间收费 (元)关于
(元)关于 (元)的函数关系式.
(元)的函数关系式.
(3)该宾馆客房部每天的利润 (元)关于
(元)关于 (元)的函数关系式;当每个房间的定价为每天多少元时,
(元)的函数关系式;当每个房间的定价为每天多少元时, 有最大值?最大值是多少?
有最大值?最大值是多少?
类型之四 存在探索性函数问题
存在型探索题是指在一定的前提下,需探索发现某种数学关系是否存在的题目.解存在性探索题先假设要探索的问题存在,继而进行推导与计算,若得出矛盾或错误的结论,则不存在,反之即为所求的结论.探索性问题由于它的题型新颖、涉及面广、综合性强、难度较大,不仅能考查学生的数学基础知识,而且能考查学生的创新意识以及发现问题、提出问题、分析问题并解决问题的能力,因而倍受关注.
2.(•莆田市)枇杷是莆田名果之一,某果园有100棵枇杷树。每棵平均产量为40千克,现准备多种一些枇杷树以提高产量,但是如果多种树,那么树与树之间的距离和每一棵数接受的阳光就会减少,根据实践经验,每多种一棵树,投产后果园中所有的枇杷树平均每棵就会减少产量0.25千克,问:增种多少棵枇杷树,投产后可以使果园枇杷的总产量最多?最多总产量是多少千克?
注:抛物线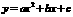 的顶点坐标是
的顶点坐标是















1.(•赣州市)年春节前夕,南方地区遭遇罕见的低温雨雪冰冻天气,赣南脐橙受灾滞销.为了减少果农的损失,政府部门出台了相关补贴政策:采取每千克补贴0.2元的办法补偿果农.
下图是“绿荫”果园受灾期间政府补助前、后脐橙销售总收入y(万元)与销售量x(吨)的关系图.请结合图象回答以下问题:
(1)在出台该项优惠政策前,脐橙的售价为每千克多少元?
(2)出台该项优惠政策后,“绿荫”果园将剩余脐橙按原售价打九折赶紧全部销完,加上政府补贴共收入11.7万元,求果园共销售了多少吨脐橙?
(3)①求出台该项优惠政策后y与x的函数关系式;②去年“绿荫”果园销售30吨,总收入为10.25万元;若按今年的销售方式,则至少要销售多少吨脐橙?总收入能达到去年水平.








类型之二 与二次函数有关的最优化问题
二次函数是一描述现实世界变量之间关系的重要数学模型.二次函数在人们的生产、生活中有着广泛的应用,求最大利润、最大面积的例子就是它在最优化问题中的应用.
7.[答案](1)EF=EB.证明:如图,以E为圆心,以EA为半径画弧交直线m于点M,连结EM.

∴EM=EA, ∴∠EMA=∠EAM.
∵BC=Kab,k=1,∴BC=AB.
∴∠CAB=∠ACB.
∵m∥n,∴∠MAC=∠ACB, ∠FAB=∠ABC.
∴∠MAC=∠CAB.
∴∠CAB=∠EMA.
∵∠BEF=∠ABC, ∴∠BEF=∠FAB.
∵∠AHF=∠EHB, ∴∠AFE=∠ABE.
∴△AEB≌△MEF.
∴EF=EB.
探索思路:如上图,∵BC=Kab,k=1,∴BC=AB.
∴∠CAB=∠ACB.
∵m∥n,∴∠MAC=∠ACB.
添加条件:∠ABC=90°.
证明:如图,在直线m上截取AM=AB,连结ME.
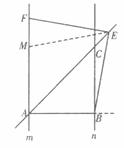
∵BC=kAB,k=1,∴BC=AB.∵∠ABC=90°, ∴∠CAB=∠ACB=45°,
∵m∥n,∴∠MAE=∠ACB=∠CAB=45°, ∠FAB=90°.
∵AE=AE, ∴△MAE≌△ABE.
∴EM=EB, ∠AME=∠ABE.
∵∠BEF=∠ABC=90°, ∴∠FAB+∠BEF=180°.
∴∠ABE+∠EFA=180°,又∵∠AME+∠EMF=180°,
∴∠EMF=∠EFA.
∴EM=EF. ∴EF=EB.
(2)EF= EB.
EB.
说明:如图,过点E作EM⊥m、EN⊥AB,垂足为M、N.
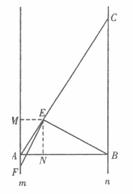
∴∠EMF=∠ENA=∠ENB=90°.
∵m∥n,∠ABC=90°, ∴∠MAB=90°.
∴四边形MENA为矩形.∴ME=NA, ∠MEN=90°.
∵∠BEF=∠ABC=90°. ∴∠MEF=∠NEB.
∴△MEF∽△NEB.
∴ ∴
∴
在Rt△ANE和Rt△ABC中,tan∠BAC=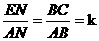 ,
,
∴EF= EB.
EB.
6.[答案]:(1)①CF与BD位置关系是 垂直、数量关系是相等;
②当点D在BC的延长线上时①的结论仍成立.
由正方形ADEF得 AD=AF ,∠DAF=90º.
∵∠BAC=90º,∴∠DAF=∠BAC , ∴∠DAB=∠FAC,
又AB=AC ,∴△DAB≌△FAC , ∴CF=BD
∠ACF=∠ABD.
∵∠BAC=90º, AB=AC ,∴∠ABC=45º,∴∠ACF=45º,
∴∠BCF=∠ACB+∠ACF= 90º.即 CF⊥BD
(2)画图正确
当∠BCA=45º时,CF⊥BD(如图丁).

理由是:过点A作AG⊥AC交BC于点G,∴AC=AG
可证:△GAD≌△CAF ∴∠ACF=∠AGD=45º
∠BCF=∠ACB+∠ACF= 90º. 即CF⊥BD
(3)当具备∠BCA=45º时,
过点A作AQ⊥BC交BC的延长线于点Q,(如图戊)

∵DE与CF交于点P时, ∴此时点D位于线段CQ上,
∵∠BCA=45º,可求出AQ= CQ=4.设CD=x ,∴ DQ=4-x,
容易说明△AQD∽△DCP,∴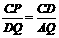 , ∴
, ∴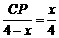 ,
,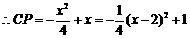 .
.
∵0<x≤3 ∴当x=2时,CP有最大值1.
5.[答案]解:(1)任选两个三角形的所有可能情况如下六种情况:①②,①③,①④,②③,②④,③④其中有两组(①③,②④)是相似的.
∴选取到的二个三角形是相似三角形的概率是P
(2)证明:选择①、③证明.
在△AOB与△COD中, ∵AB∥CD,
∴∠CDB=∠DBA , ∠DCA=∠CAB,
∴△AOB∽△COD
选择②、④证明.
∵四边形ABCD是等腰梯形, ∴∠DAB=∠CAB,
∴在△DAB与△CBA中有
AD=BC, ∠DAB=∠CAB,AB=AB,
∴△DAB ≌ △CBA,
∴∠ADO=∠BCO.
又∠DOA=∠COB, ∴△DOA∽△COB
4.[解析]考察了相似的两种基本图形,平行四边形中利用全等三角形的简单证明.
[答案](1)  AEH与
AEH与 DFH.(或
DFH.(或 AEH与
AEH与 BEG, 或
BEG, 或 BEG与
BEG与 CFG ,或
CFG ,或 DFH与
DFH与 CFG)
CFG)
(2)OE=OF.
证明: 四边形ABCD是平行四边形,
四边形ABCD是平行四边形,
 ∥CD,
∥CD,
 ,
,
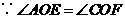 ,
,  △
△ △
△ ,
,
 .
.
3.[解析]由于A、C、E三点共线可证明三角形ACD与三角形BCE全等(边角边)从而可证AD=BE、∠AOB=∠CAD+∠CEB=∠CCBE+∠CEB =∠ACB= 60°,再证三角形ACP全等于三角形BCQ,从而可证AP=BQ,PQ∥AE。如果DE=DP,那么就会有DE=DP=EQ(三角形CEQ全等于三角形CDP)EQ=CE因为∠DCE=60°,所以三角形CEQ为等边三角形,矛盾。
[答案](1)(2)(3)(5)
2.[解析]由本题图形相似已经有一个公共角,再找一组对应角相等或公共角的两边对应成比例即可。
[答案]  ,或
,或 ,或
,或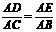
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com