
题目列表(包括答案和解析)
6、(03厦门)
如图,BD、BE分别是∠ABC与它的邻补角∠ABP的平分线,AE⊥BE,AD⊥BD,E、D为垂足.
(1)求证:四边形AEBD是矩形;
(2)若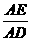 =3,F、G分别为AE、AD上的点,FG交AB于点H,且
=3,F、G分别为AE、AD上的点,FG交AB于点H,且 =3,求证:△AHG是等腰三角形.
=3,求证:△AHG是等腰三角形.

5、 .(03浙江金华)如图所示,在ΔABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x。(1)当x为何值时,PQ∥BC?(2)当
.(03浙江金华)如图所示,在ΔABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x。(1)当x为何值时,PQ∥BC?(2)当 ,求
,求 的值;(3)ΔAPQ能否与ΔCQB相似?若能,求出AP的长;若不能,请说明理由。
的值;(3)ΔAPQ能否与ΔCQB相似?若能,求出AP的长;若不能,请说明理由。
4、已知∠AOB=90°,OM是∠AOB的平分线,按以下要求解答问题:
(1) 将三角板的直角顶点P在射线OM上移动,两直角边分别与边OA,OB交于点C,D.
①在图甲中,证明:PC=PD;
②在图乙中,点G是CD与OP的交点,且PG= PD,求△POD与△PDG的面积之比.
PD,求△POD与△PDG的面积之比.
(2)将三角板的直角顶点P在射线OM上移动,一直角边与边OB交于点D,OD=1,另一直角边与直线OA,直线OB分别交于点C,E,使以P,D,E为顶点的三角形与△OCD相似,在图丙中作出图形,试求OP的长. 
3、(03广西桂林)为防水患,在漓江上游修筑了防洪堤,其横截面为一梯形(如图所示).堤的上底宽AD和提高DF都是6米,其中∠B=∠CDF. (1)求证:△ABE∽△CDF; (2)如果tanB=2,求堤的下底BC的长.

2、(02江苏盐城)已知:如图,在直角三角形ABC中,
∠BAC= 90°,AB= AC,D为BC的中点,E为AC上一点,点G在BE上,连结DG并延长交AE于F,若∠FGE= 45°,
(1)求证:BD·BC= BG·BE;
(2)求证:AG⊥BE;
(3)若E为AC的中点,求EF∶FD的值。
1、(02年湖北黄冈)已知:如图1,AB⊥BD,CD⊥BD,垂足分别为B、D,AD和BC相交于点E,EF⊥BD,垂足为F,我们可以证明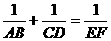 成立(不要求考生证明).
成立(不要求考生证明).
若将图1中的垂线改为斜交,如图2,AB∥CD,AD,BC相交于点E,
过点E作EF∥AB,交BD于点F,则:
(1)

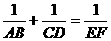 还成立吗?如果成立,请给出证明;如果不成立,请说明理由;
还成立吗?如果成立,请给出证明;如果不成立,请说明理由;
(2) 请找出S△ABD,S△BED和S△BDC间的关系式,并给出证明.

7、(03常德).如图1,D是△ABC的 BC边上的中点,过点D的一条直线交AC于F,交BA的延长线于E,AG∥BC交EF于G,我们可以证明EG·DC=ED·AG成立(不要求考生证明).
(1)如图2,若将图1中的过点D的一条直线交AC于F,改为交CA的延长线于F,交BA的延长线于E,改为交BA于E,其它条件不变,则EG·DC=ED·AG还成立吗?如果成立,请给出证明;如果不成立,请说明理由;
(2)根据图2,请你找出EG、FD、ED、FG四条线段之间的关系,并给出证明;
 (3)如图3, 若将图1中的过点D的一条直线交AC于F,改为交CA的反向延长线于F.其它条件不变,则(2)得到的结论是否成立?
(3)如图3, 若将图1中的过点D的一条直线交AC于F,改为交CA的反向延长线于F.其它条件不变,则(2)得到的结论是否成立?

6、(03厦门)
如图,BD、BE分别是∠ABC与它的邻补角∠ABP的平分线,AE⊥BE,AD⊥BD,E、D为垂足.
(1)求证:四边形AEBD是矩形;
(2)若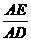 =3,F、G分别为AE、AD上的点,FG交AB于点H,且
=3,F、G分别为AE、AD上的点,FG交AB于点H,且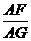 =3,求证:△AHG是等腰三角形.
=3,求证:△AHG是等腰三角形.

5、 .(03浙江金华)如图所示,在ΔABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x。(1)当x为何值时,PQ∥BC?(2)当
.(03浙江金华)如图所示,在ΔABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x。(1)当x为何值时,PQ∥BC?(2)当 ,求
,求 的值;(3)ΔAPQ能否与ΔCQB相似?若能,求出AP的长;若不能,请说明理由。
的值;(3)ΔAPQ能否与ΔCQB相似?若能,求出AP的长;若不能,请说明理由。
4、已知∠AOB=90°,OM是∠AOB的平分线,按以下要求解答问题:
(1) 将三角板的直角顶点P在射线OM上移动,两直角边分别与边OA,OB交于点C,D.
①在图甲中,证明:PC=PD;
②在图乙中,点G是CD与OP的交点,且PG= PD,求△POD与△PDG的面积之比.
PD,求△POD与△PDG的面积之比.
(2)将三角板的直角顶点P在射线OM上移动,一直角边与边OB交于点D,OD=1,另一直角边与直线OA,直线OB分别交于点C,E,使以P,D,E为顶点的三角形与△OCD相似,在图丙中作出图形,试求OP的长. 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com