6．一个数字在镜子里看是“1208”，且这个数字图像垂直对着镜子，则实际上这个数字是　　　　　 ．

5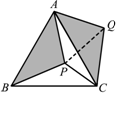．P是等边内部一点，、、

的大小之比是5:6:7，所以PA、PB、PC的长为

边的三角形的三个角的大小之比是(　 )

(A)2:3:4　　 (B)3:4:5　　

(C)4:5:6　　 (D)不能确定

3．如图，在这四个图案中都是某种衣物的洗涤说明，请指出不是

利用图形的平移、旋转和反射(轴对称)设计的是(　　 )

4．如图，一块等边三角形木板ABC的边长为1，现将木板沿水平线翻转(绕一个点旋转)，那么A点从开始到结束所走的路径长度为(　　 )

(A)4　 (B)2π　 (C)　 (D)

1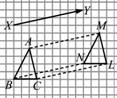．如图所示，将沿着方向平移一定的距离成为△MNL，就得到，则下列结论中正确的是(　　 )

①AM∥BN；②AM=BN；③BC=ML；④∠ACB=∠MNL

A．1个　 B．2个　 C．3个　 D．4个

8.如图,天空中有一个静止的广告气球C,从地面A 点测得C点的仰角为45°,从地面B点测得C点的仰角为60°.已知AB=20m.点C和直线AB在同一铅垂平面上,求气球离地面的高度(结果保留根号).

7.高速公路旁有一矩形坡面,其横截面如图所示,公路局为了美化公路沿线环境,决定把矩形坡面平均分成11段相间种草与栽花.已知该矩形坡面的长为550m,铅直高度AB为2m,坡度为2:1,若种草每平方米需投资20元, 栽花每平方米需投资15元,求公路局将这一坡面美化最少需投资多少元?( 结果保留三个有效数字).

6.某地有一居民楼,窗户朝南,窗户的高度为hm,此地一年中的冬至这一天的正午时刻太阳光与地面的夹角最小为a,夏至这一天的正午时刻太阳光与地面的夹角最大为 (如图1-15-23.小明想为自己家的窗户设计一个直角三角形遮阳篷BCD.要求它既能最大限度地遮挡夏天炎热的阳光, 又能最大限制地使冬天温暖的阳光射入室内.小明查阅了有关资料,获得了所在地区∠α和∠β 的相应数据:∠α=24 °36′,∠β=73°30′,小明又得窗户的高AB=1.65m.若同时满足下面两个条件,(1) 当太阳光与地面的夹角为α时,要想使太阳光刚好全部射入室内;(2) 当太阳光与地面的夹角为β时,要想使太阳光刚好不射入室内,请你借助下面的图形(如图), 帮助小明算一算,遮阳篷BCD中,BC和CD的长各是多少?(精确到0.01m)

　　 以下数据供计算中选用

　　 sin24°36′=0.416　　 cos24°36′=0.909

　　 tan24°36′=0.458　　 cot24°36′=2.184

　　 sin73°30′=0.959　　 cos73°30′=0.284

tan73°30′=3.376　　 cot73°30′=0.296

5.如图,在Rt△ABC中,a、b分别是∠A、∠B的对边,c 为斜边,如果已知两个元素a、∠B,就可以求出其余三个未知元素b、c、∠A.

　　 (1)求解的方法有多种,请你按照下列步骤,完成一种求解过程:

　　 (2)请你分别给出a、∠B的一个具体数值,然后按照(1)中的思路,求出b、c、 ∠A的值.

4.我市某区为提高某段海堤的防海潮能力,计划将长96m 的一堤段(原海堤的横断面如图中的梯形ABCD)的堤面加宽1.6m, 背水坡度由原来的1:1改成1:2,已知原背水坡长AD=8.0m,求完成这一工程所需的土方, 要求保留两个有效数字.

(注:坡度=坡面与水平面夹角的正切值;提供数据:)

3.已知,如图,A、B、C 三个村庄在一条东南走向的公路沿线上,AB=2km.在B村的正北方向有一个D村,测得∠DAB=45°,∠DCB=28°, 今将△ACD区域进行规划,除其中面积为0.5km²的水塘外,准备把剩余的一半作为绿化用地,试求绿化用地的面积.(结果精确到0.1km²,sin28°=0.469 5,cos28°=0.882 9, tan28°=0.531 7,cos28°=1.880 7)