
题目列表(包括答案和解析)
24.(08江苏扬州)(本题答案暂缺)26.(本题满分14分)
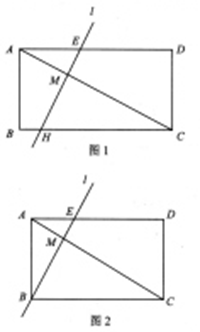
已知:矩形ABCD中,AB=1,点M在对角线AC上,直线l过点M且与AC垂直,与AD相交于点E。
(1)如果直线l与边BC相交于点H(如图1),AM= AC且AD=A,求AE的长;(用含a的代数式表示)
AC且AD=A,求AE的长;(用含a的代数式表示)
(2)在(1)中,又直线l 把矩形分成的两部分面积比为2:5,求a的值;
(3)若AM= AC,且直线l经过点B(如图2),求AD的长;
AC,且直线l经过点B(如图2),求AD的长;
(4)如果直线l分别与边AD、AB相交于点E、F,AM= AC。设AD长为x,△AEF的面积为y,求y与x的函数关系式,并指出x的取值范围。(求x的取值范围可不写过程)
AC。设AD长为x,△AEF的面积为y,求y与x的函数关系式,并指出x的取值范围。(求x的取值范围可不写过程)
23.(08江苏盐城)(本题答案暂缺)28.(本题满分12分)
如图甲,在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
解答下列问题:
(1)如果AB=AC,∠BAC=90º.
①当点D在线段BC上时(与点B不重合),如图乙,线段CF、BD之间的位置关系为 ▲ ,数量关系为 ▲ .
 ②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?
②当点D在线段BC的延长线上时,如图丙,①中的结论是否仍然成立,为什么?
(2)如果AB≠AC,∠BAC≠90º,点D在线段BC上运动.
试探究:当△ABC满足一个什么条件时,CF⊥BC(点C、F重合除外)?画出相应图形,并说明理由.(画图不写作法)
(3)若AC=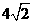 ,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.
,BC=3,在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.
22.(08江苏徐州)(本题答案暂缺)28.如图1,一副直角三角板满足AB=BC,AC=DE,∠ABC=∠DEF=90°,∠EDF=30°
[操作]将三角板DEF的直角顶点E放置于三角板ABC的斜边AC上,再将三角板DEF绕点E旋转,并使边DE与边AB交于点P,边EF与边BC于点Q
[探究一]在旋转过程中,
(1)
如图2,当 时,EP与EQ满足怎样的数量关系?并给出证明.
时,EP与EQ满足怎样的数量关系?并给出证明.
(2)
如图3,当 时EP与EQ满足怎样的数量关系?,并说明理由.
时EP与EQ满足怎样的数量关系?,并说明理由.
(3)
根据你对(1)、(2)的探究结果,试写出当 时,EP与EQ满足的数量关系式为_________,其中
时,EP与EQ满足的数量关系式为_________,其中 的取值范围是_______(直接写出结论,不必证明)
的取值范围是_______(直接写出结论,不必证明)
[探究二]若,AC=30cm,连续PQ,设△EPQ的面积为S(cm2),在旋转过程中:
(1) S是否存在最大值或最小值?若存在,求出最大值或最小值,若不存在,说明理由.
(2) 随着S取不同的值,对应△EPQ的个数有哪些变化?不出相应S值的取值范围.



21.(08江苏无锡)28.(本小题满分8分)
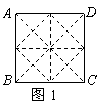
一种电讯信号转发装置的发射直径为31km.现要求:在一边长为30km的正方形城区选择若干个安装点,每个点安装一个这种转发装置,使这些装置转发的信号能完全覆盖这个城市.问:
(1)能否找到这样的4个安装点,使得这些点安装了这种转发装置后能达到预设的要求?
(2)至少需要选择多少个安装点,才能使这些点安装了这种转发装置后达到预设的要求?
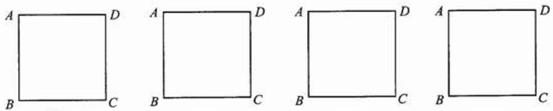
答题要求:请你在解答时,画出必要的示意图,并用必要的计算、推理和文字来说明你的理由.(下面给出了几个边长为30km的正方形城区示意图,供解题时选用)
|
|
|
|
(08江苏无锡28题解析)28.解:(1)将图1中的正方形等分成如图的四个小正方形,将这4个转发装置安装在这4个小正方形对角线的交点处,此时,每个小正方形的对角线长为 ,每个转发装置都能完全覆盖一个小正方形区域,故安装4个这种装置可以达到预设的要求.
,每个转发装置都能完全覆盖一个小正方形区域,故安装4个这种装置可以达到预设的要求.
·························································································· (3分)(图案设计不唯一)
(2)将原正方形分割成如图2中的3个矩形,使得 .将每个装置安装在这些矩形的对角线交点处,设
.将每个装置安装在这些矩形的对角线交点处,设 ,则
,则 ,
, .
.
由 ,得
,得 ,
,
 ,
,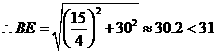 ,
,
即如此安装3个这种转发装置,也能达到预设要求.········································ (6分)
或:将原正方形分割成如图2中的3个矩形,使得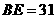 ,
,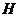 是
是 的中点,将每个装置安装在这些矩形的对角线交点处,则
的中点,将每个装置安装在这些矩形的对角线交点处,则 ,
, ,
,  ,即如此安装三个这个转发装置,能达到预设要求.················································································· (6分)
,即如此安装三个这个转发装置,能达到预设要求.················································································· (6分)
要用两个圆覆盖一个正方形,则一个圆至少要经过正方形相邻两个顶点.如图3,用一个直径为31的 去覆盖边长为30的正方形
去覆盖边长为30的正方形 ,设
,设 经过
经过 ,
, 与
与 交于
交于 ,连
,连 ,则
,则 ,这说明用两个直径都为31的圆不能完全覆盖正方形
,这说明用两个直径都为31的圆不能完全覆盖正方形 .
.
所以,至少要安装3个这种转发装置,才能达到预设要求.····························· (8分)
评分说明:示意图(图1、图2、图3)每个图1分.


20.(08江苏无锡)27.(本小题满分10分)
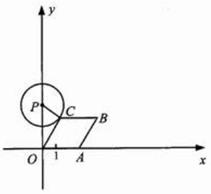
如图,已知点 从
从 出发,以1个单位长度/秒的速度沿
出发,以1个单位长度/秒的速度沿 轴向正方向运动,以
轴向正方向运动,以 为顶点作菱形
为顶点作菱形 ,使点
,使点 在第一象限内,且
在第一象限内,且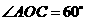 ;以
;以 为圆心,
为圆心, 为半径作圆.设点
为半径作圆.设点 运动了
运动了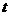 秒,求:
秒,求:
(1)点 的坐标(用含
的坐标(用含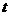 的代数式表示);
的代数式表示);
(2)当点 在运动过程中,所有使
在运动过程中,所有使 与菱形
与菱形 的边所在直线相切的
的边所在直线相切的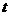 的值.
的值.
(08江苏无锡27题解析)27.解:(1)过 作
作 轴于
轴于 ,
,
 ,
, ,
,
 ,
,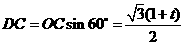 ,
,
 点
点 的坐标为
的坐标为 .········ (2分)
.········ (2分)
 (2)①当
(2)①当 与
与 相切时(如图1),切点为
相切时(如图1),切点为 ,此时
,此时 ,
,

 ,
, ,
,
 .·············· (4分)
.·············· (4分)
②当 与
与 ,即与
,即与 轴相切时(如图2),则切点为
轴相切时(如图2),则切点为 ,
,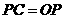 ,
,
过 作
作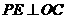 于
于 ,则
,则 ,······················································· (5分)
,······················································· (5分)
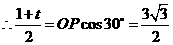 ,
, .················································· (7分)
.················································· (7分)
③当 与
与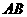 所在直线相切时(如图3),设切点为
所在直线相切时(如图3),设切点为 ,
, 交
交 于
于 ,
,
则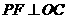 ,
, ,
,
 .··························································· (8分)
.··························································· (8分)
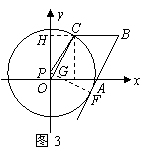 过
过 作
作 轴于
轴于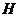 ,则
,则 ,
,
 ,
,
化简,得 ,
,
解得 ,
,
 ,
,
 .
.
 所求
所求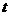 的值是
的值是 ,
, 和
和 .··································· (10分)
.··································· (10分)
19.(08江苏泰州)29.已知二次函数 的图象经过三点(1,0),(-3,0),(0,
的图象经过三点(1,0),(-3,0),(0,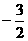 )。
)。
(1)求二次函数的解析式,并在给定的直角坐标系中作出这个函数的图像;(5分)
(2)若反比例函数 图像与二次函数
图像与二次函数 的图像在第一象限内交于点A(x0,y0), x0落在两个相邻的正整数之间。请你观察图像,写出这两个相邻的正整数;(4分)
的图像在第一象限内交于点A(x0,y0), x0落在两个相邻的正整数之间。请你观察图像,写出这两个相邻的正整数;(4分)
(3)若反比例函数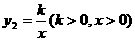 的图像与二次函数
的图像与二次函数 的图像在第一象限内的交点为A,点A的横坐标为
的图像在第一象限内的交点为A,点A的横坐标为 满足2<
满足2< <3,试求实数k的取值范围。(5分)
<3,试求实数k的取值范围。(5分)
(08江苏泰州29题解析)九、(本题满分14分)29(1)设抛物线解析式为y=a(x-1)(x+3)…………………………1分
(只要设出解析式正确,不管是什么形式给1分)
将(0,- )代入,解得a=
)代入,解得a= .
.
∴抛物线解析式为y= x2+x-
x2+x- …………………………………3分
…………………………………3分
(无论解析式是什么形式只要正确都得分)
画图(略)。(没有列表不扣分)…………………………………5分
(2)正确的画出反比例函数在第一象限内的图像……………7分
由图像可知,交点的横坐标x0 落在1和2之间,从而得出这两个相邻的正整数为1与2。…………………………………………………9分
(3)由函数图像或函数性质可知:当2<x<3时,
对y1= x2+x-
x2+x- , y1随着x增大而增大,对y2=
, y1随着x增大而增大,对y2=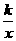 (k>0),
(k>0),
y2随着X的增大而减小。因为A(X0,Y0)为二次函数图像与反比例函数图像的交点,所心当X0=2时,由反比例函数图象在二次函数上方得y2>y1,
即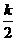 >
> ×22+2-
×22+2- ,解得K>5。…………………………………11分
,解得K>5。…………………………………11分
同理,当X0=3时,由二次函数数图象在反比例上方得y1>y2,
即 ×32+3-
×32+3- >
>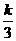 ,解得K<18。…………………………………13
,解得K<18。…………………………………13
所以K的取值范围为5 <K<18………………………………………14分
18.(08江苏宿迁)27.(本题满分12分)
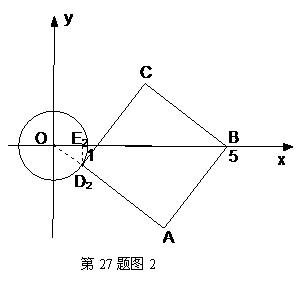
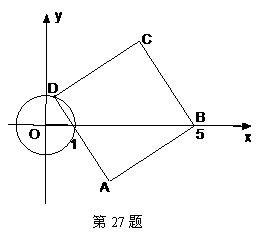 如图,⊙
如图,⊙ 的半径为
的半径为 ,正方形
,正方形 顶点
顶点 坐标为
坐标为 ,顶点
,顶点 在⊙
在⊙ 上运动.
上运动.
(1)当点 运动到与点
运动到与点 、
、 在同一条直线上时,试证明直线
在同一条直线上时,试证明直线 与⊙
与⊙ 相切;
相切;
(2)当直线 与⊙
与⊙ 相切时,求
相切时,求 所在直线对应的函数关系式;
所在直线对应的函数关系式;
(3)设点 的横坐标为
的横坐标为 ,正方形
,正方形 的面积为
的面积为 ,求
,求 与
与 之间的函数关系式,并求出
之间的函数关系式,并求出 的最大值与最小值.
的最大值与最小值.
(08江苏宿迁27题解析)27.解:(1) ∵四边形 为正方形
∴
为正方形
∴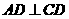
∵ 、
、 、
、 在同一条直线上 ∴
在同一条直线上 ∴ ∴直线
∴直线 与⊙
与⊙ 相切;
相切;
 (2)直线
(2)直线 与⊙
与⊙ 相切分两种情况:
相切分两种情况:
①如图1,
设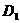 点在第二象限时,过
点在第二象限时,过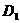 作
作 轴于点
轴于点 ,设此时的正方形的边长为
,设此时的正方形的边长为 ,则
,则 ,解得
,解得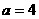 或
或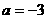 (舍去).
(舍去).
由 ∽
∽ 得
得
 ∴
∴ ∴
∴ ,
,
故直线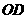 的函数关系式为
的函数关系式为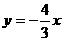 ;
;
②如图2, 设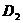 点在第四象限时,过
点在第四象限时,过 作
作 轴于点
轴于点 ,设此时的正方形的边长为
,设此时的正方形的边长为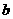 ,则
,则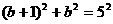 ,解得
,解得 或
或 (舍去).
(舍去).
由 ∽
∽ 得
得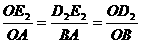
∴ ∴
∴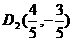 ,故直线
,故直线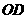 的函数关系式为
的函数关系式为 .
.
(3)设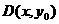 ,则
,则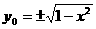 ,由
,由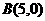 得
得
∴
∵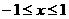
∴ .
.
17.(08江苏南通)(第28题14分)28.已知双曲线 与直线
与直线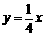 相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线
相交于A、B两点.第一象限上的点M(m,n)(在A点左侧)是双曲线 上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线
上的动点.过点B作BD∥y轴交x轴于点D.过N(0,-n)作NC∥x轴交双曲线 于点E,交BD于点C.
于点E,交BD于点C.
(1)若点D坐标是(-8,0),求A、B两点坐标及k的值.
(2)若B是CD的中点,四边形OBCE的面积为4,求直线CM的解析式.
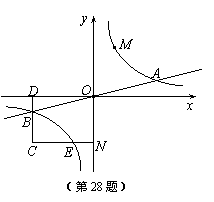 (3)设直线AM、BM分别与y轴相交于P、Q两点,且MA=pMP,MB=qMQ,求p-q的值.
(3)设直线AM、BM分别与y轴相交于P、Q两点,且MA=pMP,MB=qMQ,求p-q的值.
(08江苏南通28题解析)28.解:(1)∵D(-8,0),
∴B点的横坐标为-8,代入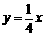 中,得y=-2.
中,得y=-2.
∴B点坐标为(-8,-2).而A、B两点关于原点对称,∴A(8,2).
从而 .……………………3分
.……………………3分
(2)∵N(0,-n),B是CD的中点,A、B、M、E四点均在双曲线上,
∴ ,B(-2m,-
,B(-2m,- ),C(-2m,-n),E(-m,-n). ……4分
),C(-2m,-n),E(-m,-n). ……4分
S矩形DCNO ,S△DBO=
,S△DBO= ,S△OEN
=
,S△OEN
= , …………7分
, …………7分
∴S四边形OBCE=
S矩形DCNO-S△DBO- S△OEN=k.∴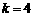 . ……………………8分
. ……………………8分
由直线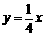 及双曲线
及双曲线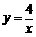 ,得A(4,1),B(-4,-1),
,得A(4,1),B(-4,-1),
∴C(-4,-2),M(2,2).………………………………………………9分
设直线CM的解析式是 ,由C、M两点在这条直线上,得
,由C、M两点在这条直线上,得
 解得
解得 .
.
∴直线CM的解析式是 .………………………………………11分
.………………………………………11分
(3)如图,分别作AA1⊥x轴,MM1⊥x轴,垂足分别为A1、M1.
 设A点的横坐标为a,则B点的横坐标为-a.于是
设A点的横坐标为a,则B点的横坐标为-a.于是
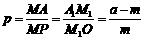 .
.
同理 ,…………13分
,…………13分
∴ .……………14分
.……………14分
15.(08江苏连云港)25.(本小题满分12分)
我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段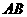 的最小覆盖圆就是以线段
的最小覆盖圆就是以线段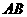 为直径的圆.
为直径的圆.
 (1)请分别作出图1中两个三角形的最小覆盖圆(要求用尺规作图,保留作图痕迹,不写作法);
(1)请分别作出图1中两个三角形的最小覆盖圆(要求用尺规作图,保留作图痕迹,不写作法);
(2)探究三角形的最小覆盖圆有何规律?请写出你所得到的结论(不要求证明);
 (3)某地有四个村庄
(3)某地有四个村庄 (其位置如图2所示),现拟建一个电视信号中转站,为了使这四个村庄的居民都能接收到电视信号,且使中转站所需发射功率最小(距离越小,所需功率越小),此中转站应建在何处?请说明理由.
(其位置如图2所示),现拟建一个电视信号中转站,为了使这四个村庄的居民都能接收到电视信号,且使中转站所需发射功率最小(距离越小,所需功率越小),此中转站应建在何处?请说明理由.
(08江苏连云港25题解析)25.解:(1)如图所示:················································ 4分

(注:正确画出1个图得2分,无作图痕迹或痕迹不正确不得分)
(2)若三角形为锐角三角形,则其最小覆盖圆为其外接圆;·································· 6分
若三角形为直角或钝角三角形,则其最小覆盖圆是以三角形最长边(直角或钝角所对的边)为直径的圆. 8分
(3)此中转站应建在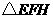 的外接圆圆心处(线段
的外接圆圆心处(线段 的垂直平分线与线段
的垂直平分线与线段 的垂直平分线的交点处). 10分
的垂直平分线的交点处). 10分
理由如下:
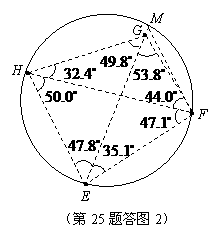 由
由 ,
,
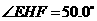 ,
, ,
,
故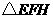 是锐角三角形,
是锐角三角形,
所以其最小覆盖圆为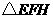 的外接圆,
的外接圆,
设此外接圆为 ,直线
,直线 与
与 交于点
交于点 ,
,
则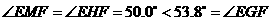 .
.
故点 在
在 内,从而
内,从而 也是四边形
也是四边形 的最小覆盖圆.
的最小覆盖圆.
所以中转站建在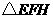 的外接圆圆心处,能够符合题中要求.
的外接圆圆心处,能够符合题中要求.
·················································································· 12分
 16(08江苏南京)28.(10分)一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为
16(08江苏南京)28.(10分)一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为 ,两车之间的距离为
,两车之间的距离为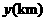 ,图中的折线表示
,图中的折线表示 与
与 之间的函数关系.
之间的函数关系.
根据图象进行以下探究:
信息读取
(1)甲、乙两地之间的距离为 km;
(2)请解释图中点 的实际意义;
的实际意义;
图象理解
(3)求慢车和快车的速度;
(4)求线段 所表示的
所表示的 与
与 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量 的取值范围;
的取值范围;
问题解决
(5)若第二列快车也从甲地出发驶往乙地,速度与第一列快车相同.在第一列快车与慢车相遇30分钟后,第二列快车与慢车相遇.求第二列快车比第一列快车晚出发多少小时?
(08江苏南京28题解析)28.(本题10分)
解:(1)900;········································································································ 1分
(2)图中点 的实际意义是:当慢车行驶4h时,慢车和快车相遇.······················ 2分
的实际意义是:当慢车行驶4h时,慢车和快车相遇.······················ 2分
(3)由图象可知,慢车12h行驶的路程为900km,
所以慢车的速度为 ;··································································· 3分
;··································································· 3分
当慢车行驶4h时,慢车和快车相遇,两车行驶的路程之和为900km,所以慢车和快车行驶的速度之和为 ,所以快车的速度为150km/h.······················································· 4分
,所以快车的速度为150km/h.······················································· 4分
(4)根据题意,快车行驶900km到达乙地,所以快车行驶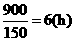 到达乙地,此时两车之间的距离为
到达乙地,此时两车之间的距离为 ,所以点
,所以点 的坐标为
的坐标为 .
.
设线段 所表示的
所表示的 与
与 之间的函数关系式为
之间的函数关系式为 ,把
,把 ,
, 代入得
代入得

解得
所以,线段 所表示的
所表示的 与
与 之间的函数关系式为
之间的函数关系式为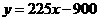 .·················· 6分
.·················· 6分
自变量 的取值范围是
的取值范围是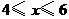 .········································································ 7分
.········································································ 7分
(5)慢车与第一列快车相遇30分钟后与第二列快车相遇,此时,慢车的行驶时间是4.5h.
把 代入
代入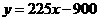 ,得
,得 .
.
此时,慢车与第一列快车之间的距离等于两列快车之间的距离是112.5km,所以两列快车出发的间隔时间是 ,即第二列快车比第一列快车晚出发0.75h.···························· 10分
,即第二列快车比第一列快车晚出发0.75h.···························· 10分
14.(08江苏连云港)24.(本小题满分14分)
如图,现有两块全等的直角三角形纸板Ⅰ,Ⅱ,它们两直角边的长分别为1和2.将它们分别放置于平面直角坐标系中的 ,
, 处,直角边
处,直角边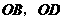 在
在 轴上.一直尺从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至
轴上.一直尺从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至 处时,设
处时,设 与
与 分别交于点
分别交于点 ,与
,与 轴分别交于点
轴分别交于点 .
.
(1)求直线 所对应的函数关系式;
所对应的函数关系式;
(2)当点 是线段
是线段 (端点除外)上的动点时,试探究:
(端点除外)上的动点时,试探究:
①点 到
到 轴的距离
轴的距离 与线段
与线段 的长是否总相等?请说明理由;
的长是否总相等?请说明理由;
 ②两块纸板重叠部分(图中的阴影部分)的面积
②两块纸板重叠部分(图中的阴影部分)的面积 是否存在最大值?若存在,求出这个最大值及
是否存在最大值?若存在,求出这个最大值及 取最大值时点
取最大值时点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(08江苏连云港24题解析)24.解:(1)由直角三角形纸板的两直角边的长为1和2,
知 两点的坐标分别为
两点的坐标分别为 .
.
设直线 所对应的函数关系式为
所对应的函数关系式为 .······················································ 2分
.······················································ 2分
有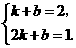 解得
解得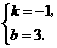
 所以,直线
所以,直线 所对应的函数关系式为
所对应的函数关系式为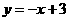 .··············································· 4分
.··············································· 4分
(2)①点 到
到 轴距离
轴距离 与线段
与线段 的长总相等.
的长总相等.
因为点 的坐标为
的坐标为 ,
,
所以,直线 所对应的函数关系式为
所对应的函数关系式为 .
.
又因为点 在直线
在直线 上,
上,
所以可设点 的坐标为
的坐标为 .
.
过点 作
作 轴的垂线,设垂足为点
轴的垂线,设垂足为点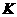 ,则有
,则有 .
.
因为点 在直线
在直线 上,所以有
上,所以有 .················· 6分
.················· 6分
因为纸板为平行移动,故有 ,即
,即 .
.
又 ,所以
,所以 .
.
法一:故 ,
,
从而有 .
.
得 ,
, .
.
所以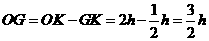 .
.
又有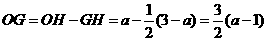 .·················································· 8分
.·················································· 8分
所以 ,得
,得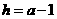 ,而
,而 ,
,
从而总有 .······························································································· 10分
.······························································································· 10分
法二:故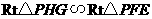 ,可得
,可得 .
.
故 .
.
所以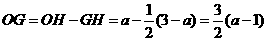 .
.
故 点坐标为
点坐标为 .
.
设直线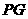 所对应的函数关系式为
所对应的函数关系式为 ,
,
则有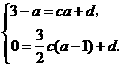 解得
解得
所以,直线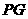 所对的函数关系式为
所对的函数关系式为 .········································ 8分
.········································ 8分
将点 的坐标代入,可得
的坐标代入,可得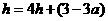 .解得
.解得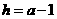 .
.
而 ,从而总有
,从而总有 .··················································· 10分
.··················································· 10分
②由①知,点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 .
.


 .······························································· 12分
.······························································· 12分
当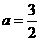 时,
时, 有最大值,最大值为
有最大值,最大值为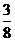 .
.
 取最大值时点
取最大值时点 的坐标为
的坐标为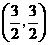 .··································································· 14分
.··································································· 14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com