
题目列表(包括答案和解析)
1、(08台州)在数学学习中,及时对知识进行归纳和整
理是改善学习的重要方法.善于学习的小明在学习了
一次方程(组)、一元一次不等式和一次函数后,把相
关知识归纳整理如下:

(1)请你根据以上方框中的内容在下面数字序号后写出相应的结论:
① ;② ;③ ;④ ;
(2)如果点 的坐标为
的坐标为 ,那么不等式
,那么不等式 的解集是
.
的解集是
.
22、(C组)2004福建南平

21、(B组)2004苏州
某中学为筹备校庆活动,准备印制一批校庆纪念册。该纪念册每册需要10张8K大小的纸,其中4张为彩页,6张为黑白页。印制该纪念册的总费用由制版费和印刷费两部分组成,制版费与印数无关,价格为:彩页300元/张,黑白页50元/张;印刷费与印数的关系见下表。
|
印数a
(单位:千册) |
1≤a<5 |
5≤a<10 |
|
彩色 (单位:元/张) |
2.2 |
2.0 |
|
黑白(单位:元/张) |
0.7 |
0.6 |
(1)印制这批纪念册的制版费为 元;(2)若印制2千册,则共需多少费用?
(3)如果该校希望印数至少为4千册,总费用至多为60000元,求印数的取值范围。(精确到0.01千册)
15、(C组)2004湖北黄岗

² 题型四 一次函数的应用问题
涉及面广,是近年中考试题中的热点题型。
基本思路是先要确立实际问题中变量间的函数关系,再解决实际问题
很多问题的两个变量之间的存在对应关系,但要建立函数解析式,却要深入探索变量之间存在的能够表示的数量关系,这是老问题,却是值得探究的新问题。
2004年中考举例
16、(A组)贵阳实验区2004
某影碟出租店开设两种租碟方式:一种是零星租碟,每张收费1元;另一种是会员卡租碟,办卡费每月12元,租碟费每张0.4元 . 小彬经常来该店租碟,若每月租碟数量为x张.
(1)写出零星租碟方式应付金额y1(元)与租碟数量x(张)之间的函数关系式;(2分)
(2)写出会员卡租碟方式应付金额y2(元 )与租碟数量x(张)之间的函数关系式;(2分)
(3)小彬选取哪种租碟方式更合算?(4分)
17、(B组)贵阳实验区2004
某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
|
x(元) |
15 |
20 |
30 |
… |
|
y(件) |
25 |
20 |
10 |
… |
若日销售量y是销售价x的一次函数.
(A组)(1)求出日销售量y(件)与销售价x(元)的函数关系式;(6分)
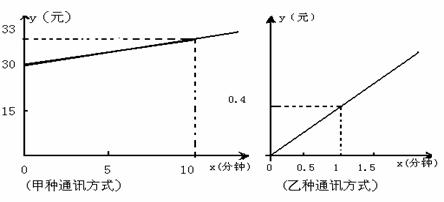 (B组)(2)要使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日销售利润是多少元?
(B组)(2)要使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日销售利润是多少元?
18、(B组)[茂名市2004年]
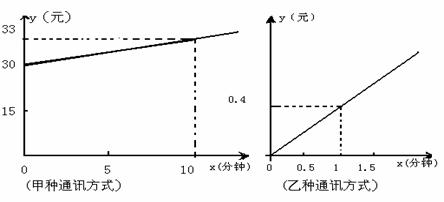
某电信部门新开设甲、乙两种通讯方式,它们的通话费 (元)与通话时间
(元)与通话时间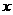 (分钟)之间的函数关系图象分别如下图:
(分钟)之间的函数关系图象分别如下图:
请你根据图象解答下列的问题:
(1)写出甲、乙两种通讯方式的通话费 (元)与通话时间
(元)与通话时间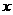 (分钟)之间的函数关系式;
(分钟)之间的函数关系式;
(2)若某人一个月内预计使用话费180元,则他应选择哪种通讯方式较合算?并说明理由。
19、(B组)[2004年芜湖市]某纺织厂生产的产品,原来每件出厂价为80元,成本为60元.由于在生产过程中平均每生产一件产品有0.5米3的污水排出,现在为了保护环境,需对污水净化处理后再排出.已知每处理1米3污水的费用为2元,且每月排污设备损耗为8000元.设现在该厂每月生产产品x件,每月纯利润y元:
① 求出y与x的函数关系式.(纯利润=总收入-总支出)
② 当y=106000时,求该厂在这个月中生产产品的件数.
20. (B组) [2004年芜湖市]
某商场在促销期间规定:商场内所有商品按标价的80%出售,同时,当顾客在该商场内消费满一定金额后,按如下方案获得相应金额的奖券.(奖券购物不再享受优惠)
|
消费金额x的范围(元) |
200≤x<400 |
400≤x<500 |
500≤x<700 |
… |
|
获得奖券的金额(元) |
30 |
60 |
100 |
… |
根据上述促销方法,顾客在该商场购物可获得双重优惠,如果胡老师在该商场购标价450元的商品,他获得的优惠额为_________元.
22、(C组)2004福建南平

21、(B组)2004苏州
某中学为筹备校庆活动,准备印制一批校庆纪念册。该纪念册每册需要10张8K大小的纸,其中4张为彩页,6张为黑白页。印制该纪念册的总费用由制版费和印刷费两部分组成,制版费与印数无关,价格为:彩页300元/张,黑白页50元/张;印刷费与印数的关系见下表。
|
印数a
(单位:千册) |
1≤a<5 |
5≤a<10 |
|
彩色 (单位:元/张) |
2.2 |
2.0 |
|
黑白(单位:元/张) |
0.7 |
0.6 |
(1)印制这批纪念册的制版费为 元;(2)若印制2千册,则共需多少费用?
(3)如果该校希望印数至少为4千册,总费用至多为60000元,求印数的取值范围。(精确到0.01千册)
15、(C组)2004湖北黄岗
² 题型四 一次函数的应用问题
涉及面广,是近年中考试题中的热点题型。
基本思路是先要确立实际问题中变量间的函数关系,再解决实际问题
很多问题的两个变量之间的存在对应关系,但要建立函数解析式,却要深入探索变量之间存在的能够表示的数量关系,这是老问题,却是值得探究的新问题。
2004年中考举例
16、(A组)贵阳实验区2004
某影碟出租店开设两种租碟方式:一种是零星租碟,每张收费1元;另一种是会员卡租碟,办卡费每月12元,租碟费每张0.4元 . 小彬经常来该店租碟,若每月租碟数量为x张.
(1)写出零星租碟方式应付金额y1(元)与租碟数量x(张)之间的函数关系式;(2分)
(2)写出会员卡租碟方式应付金额y2(元 )与租碟数量x(张)之间的函数关系式;(2分)
(3)小彬选取哪种租碟方式更合算?(4分)
17、(B组)贵阳实验区2004
某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
|
x(元) |
15 |
20 |
30 |
… |
|
y(件) |
25 |
20 |
10 |
… |
若日销售量y是销售价x的一次函数.
(A组)(1)求出日销售量y(件)与销售价x(元)的函数关系式;(6分)
 (B组)(2)要使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日销售利润是多少元?
(B组)(2)要使每日的销售利润最大,每件产品的销售价应定为多少元?此时每日销售利润是多少元?
18、(B组)[茂名市2004年]
某电信部门新开设甲、乙两种通讯方式,它们的通话费 (元)与通话时间
(元)与通话时间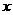 (分钟)之间的函数关系图象分别如下图:
(分钟)之间的函数关系图象分别如下图:
请你根据图象解答下列的问题:
(1)写出甲、乙两种通讯方式的通话费 (元)与通话时间
(元)与通话时间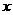 (分钟)之间的函数关系式;
(分钟)之间的函数关系式;
(2)若某人一个月内预计使用话费180元,则他应选择哪种通讯方式较合算?并说明理由。
19、(B组)[2004年芜湖市]某纺织厂生产的产品,原来每件出厂价为80元,成本为60元.由于在生产过程中平均每生产一件产品有0.5米3的污水排出,现在为了保护环境,需对污水净化处理后再排出.已知每处理1米3污水的费用为2元,且每月排污设备损耗为8000元.设现在该厂每月生产产品x件,每月纯利润y元:
① 求出y与x的函数关系式.(纯利润=总收入-总支出)
② 当y=106000时,求该厂在这个月中生产产品的件数.
20. (B组) [2004年芜湖市]
某商场在促销期间规定:商场内所有商品按标价的80%出售,同时,当顾客在该商场内消费满一定金额后,按如下方案获得相应金额的奖券.(奖券购物不再享受优惠)
|
消费金额x的范围(元) |
200≤x<400 |
400≤x<500 |
500≤x<700 |
… |
|
获得奖券的金额(元) |
30 |
60 |
100 |
… |
根据上述促销方法,顾客在该商场购物可获得双重优惠,如果胡老师在该商场购标价450元的商品,他获得的优惠额为_________元.
例6
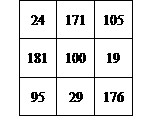
如图,在 方格内已填好了两个数19和95,可以在其余的方格中填上适当的数,使每一行、每一列、以及每一条对角线上的三个数的和都相等,
方格内已填好了两个数19和95,可以在其余的方格中填上适当的数,使每一行、每一列、以及每一条对角线上的三个数的和都相等,
(1)求x;
(2)在题设的基础上,如果中间的空格上是100,请完成填图。
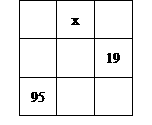
解:(1)设每一行、每一列、每一条对角线的三个数都相等的数是k
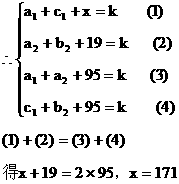

(2)中间填上100,从而不难求每行、每列、每条对角线的三个数的和为300,则其余空格上数字如图。
例5
对应实数x,y,设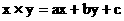 ,等式右边是通常的加法和乘法,且
,等式右边是通常的加法和乘法,且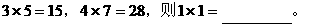
解:由题意,得

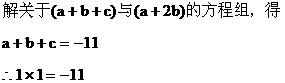
例1
对于任意实数m,等式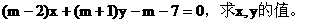
解: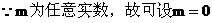

例2
关于x的代数式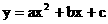 ,当x分别取1,2,-1时,y的值分别是4,7,10,求a,b,c的值。
,当x分别取1,2,-1时,y的值分别是4,7,10,求a,b,c的值。
解:根据题意,得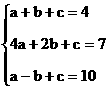
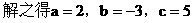
例3
已知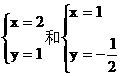 都是关于x,y的某个二元一次方程的解,求这个二元一次方程。
都是关于x,y的某个二元一次方程的解,求这个二元一次方程。
解:设这个二元一次方程为


例4
已知等式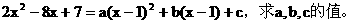
解:由已知条件得
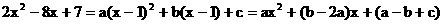
比较对应项的系数,得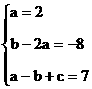
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com